
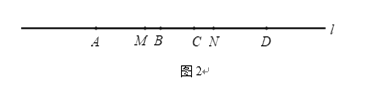
����Ŀ����ͼ1����A��B��C��DΪֱ��l�ϴ�����˳�ε�4���㣮

(1) ��ֱ��l����A��B��C��DΪ�˵���߶ι��� ����
����AC=5cm��BD=6cm��BC=1cm����PΪֱ��l��һ�㣬��PA+PD����СֵΪ cm��(2)����A��ֱ��l�������˶����߶�BD��ֱ��l�������˶���M��N�ֱ�ΪAC��BD���е㣨��ͼ2������ָ���ڴ˹������߶�AD��BC��MN�к�������ϵ��˵�����ɣ�
(3)��C��AD��һ�����ȷֵ㣬DC��AC����AD=9cm��E��F����ͬʱ��C��D�������ֱ���2cm/s��1cm/s���ٶ���ֱ��l�����˶���QΪEF���е㣬���˶�ʱ��Ϊt����AQ+AE+AF=![]() ADʱ����ֱ��д��t��ֵ��
ADʱ����ֱ��д��t��ֵ��
���𰸡�(1) ��6������10��(2)![]() ��֤����������(3)
��֤����������(3) ![]() .
.
��������
��1���������߶εĶ�����ͼ�μ��ɵó��𰸣���PA+PD��С����PΪAD���е㣬���AD�ij����ɣ�
(2) ����M��N�ֱ�ΪAC��BD���е㣬�õ�![]() ��
��![]() ������
������![]() ���뻯�ɣ�
���뻯�ɣ�
(3) ����C��AD��һ�����ȷֵ㣬DC��AC����AD=9cm���õ�![]() ��
��![]() �����ɵõ�
�����ɵõ�![]() ��
��![]() ��
��![]() ������AQ+AE+AF=
������AQ+AE+AF=![]() AD������������t.
AD������������t.
�⣺(1) ���߶��У�AB��AC��AD��BC��BD��CD����6����
�ڡ�BD=6��BC=1��
��CD=BD-BC=6-1=5��
��PA+PD��ֵ��Сʱ��PΪAD���е㣬
��![]() ��
��
(2)![]() .
.
��ͼ2ʾ��
��M��N�ֱ�ΪAC��BD���е㣬
��![]() ��
��![]()
��![]()
![]()
![]()
![]()
![]() ��
��
(3)��ͼʾ��

��C��AD��һ�����ȷֵ㣬DC��AC����AD=9cm��
��![]() ��
��![]() ��
��
����E��F����ͬʱ��C��D�������ٶ���2cm/s��1cm/s��QΪEF���е㣬�˶�ʱ��Ϊt��
����![]() ��
��![]() ��
��![]()
��AQ+AE+AF=![]() ADʱ��
ADʱ��
����![]()
���ǣ�![]()
��֮�ã�![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij����һ�鳤Ϊ(3a+b)�ס���Ϊ(2a+b)�ij����εؿ飬�м��DZ߳�Ϊ(a+b)�������Σ��滮���żƻ������м����������һ���������ܵ���Ӱ���ֽ����̻���
(1)�̻�������Ƕ���ƽ���ף�(�ú���ĸa��b��ʽ�ӱ�ʾ)
(2)�����a��10��b��12ʱ���̻������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧ��ȡ20��ѧ��ͳ��ij�µ��ñ����������������±���
�ñ�����֧�� | 4 | 5 | 6 | 8 | 9 |
ѧ���� | 4 | 4 | 7 | 3 | 2 |
�������20��ѧ������µ��ñ�����������������˵����ȷ����( ) ��
A. ������7֧ B. ��λ����6֧ C. ƽ������5֧ D. ����Ϊ0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵�����ٷ��Ų�ͬ����������Ϊ�෴�����ڶ����������ˣ��������ĸ���Ϊ������ʱ��Ϊ��������A��M��B������ͬһֱ���ϣ���AM=![]() AB����MΪ�߶�AB���е㣻�ܱ�һ���۽�С90���Ľ�һ��������۽ǵIJ��ǻ��࣮������ȷ�ĸ���Ϊ�� ��
AB����MΪ�߶�AB���е㣻�ܱ�һ���۽�С90���Ľ�һ��������۽ǵIJ��ǻ��࣮������ȷ�ĸ���Ϊ�� ��
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x1��x2��x3����x2016���Dz�����0������������y1=![]() ����y1��ֵ��
����y1��ֵ��
��x1��0ʱ��y1=![]() =
=![]() =1����x1��0ʱ��y1=
=1����x1��0ʱ��y1=![]() =
=![]() =��1������y1=��1
=��1������y1=��1
��1����y2=![]() +
+![]() ����y2��ֵ
����y2��ֵ
��2����y3=![]() +
+![]() +
+![]() ����y3��ֵΪ�� ����
����y3��ֵΪ�� ����
��3��������̽�����룬y2016=![]() +
+![]() +
+![]() +��+
+��+![]() ������ ������ͬ��ֵ����y2016��Щ��ͬ��ֵ�У�����ֵ����С��ֵ�IJ������ ����
������ ������ͬ��ֵ����y2016��Щ��ͬ��ֵ�У�����ֵ����С��ֵ�IJ������ ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��������װ�к졢�ơ���������ɫ��ƹ������ɫ���������ͬ�������а������1������������������һ�����ǰ���ĸ�����![]() ��
��
��1�������к���ĸ�����
��2���ȴӰ�������������һ���������ɫ��Żأ��ٴӰ�������������һ��������������������ɫ��ͬ�ĸ��ʣ�������ͼ���б�����⣩��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ����ȫ��ѧ����������д��������ÿλѧ����д����39���������ȡ�˲���ѧ������д��������Ƴ����µ�ͼ����

����������Ϣ����������⣺
��1��ͳ�Ʊ��е�m= ��n= ������ȫ����ͳ��ͼ��
��2������ͳ��ͼ�С�C�顱����Ӧ��Բ�ĽǵĶ����� ��
��3����֪��У����900��ѧ���������д��ȷ���ֵĸ�������24����Ϊ���ϸ�������Ƹ�У������д�������ϸ��ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڴ�СΪ4��4�������������У������������ε��ǣ�������

A. ������ B. ������ C. ������ D. ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���D��E��F�ֱ���AB��BC��AC���е㣬����DE��EF��DF��������˵������ȷ���ǣ�������
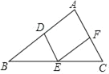
A. S��DEF��![]() S��ABC
S��ABC
B. ��DEF�ա�FAD�ա�EDB�ա�CFE
C. �ı���ADEF���ı���DBEF���ı���DECF����ƽ���ı���
D. �ı���ADEF���ܳ����ı���DBEF���ܳ����ı���DECF���ܳ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com