
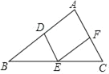
【题目】如图,在△ABC中,点D,E,F分别是AB,BC,AC的中点,连接DE,EF,DF,则下列说法不正确的是( )
A. S△DEF=![]() S△ABC
S△ABC
B. △DEF≌△FAD≌△EDB≌△CFE
C. 四边形ADEF,四边形DBEF,四边形DECF都是平行四边形
D. 四边形ADEF的周长=四边形DBEF的周长=四边形DECF的周长
【答案】D
【解析】
根据中位线定理可证DE∥AC,DF∥BC,EF∥AB,即可得四边形ADEF,四边形DECF,四边形BDFE是平行四边形.即可判断各选项是否正确.
连接DF

∵点D,E,F分别是AB,BC,AC的中点
∴DE∥AC,DF∥BC,EF∥AB
∴四边形ADEF,四边形DECF,四边形BDFE是平行四边形
∴△ADF≌△DEF,△BDE≌△DEF,△CEF≌△DEF
∴△DEF≌△ADF≌△BDE≌△CEF
∴S△ADF=S△BDE=S△DEF=S△CEF.
∴S△DEF=![]() S△ABC.
S△ABC.
故①②③说法正确
∵四边形ADEF的周长为2(AD+DE)
四边形BDFE的周长为2(BD+DF)
且AD=BD,DE≠DF,
∴四边形ADEF的周长≠四边形BDFE的周长
故④说法错误
故选:D.


科目:初中数学 来源: 题型:
【题目】如图1,点A,B,C,D为直线l上从左到右顺次的4个点.

(1) ①直线l上以A,B,C,D为端点的线段共有 条;
②若AC=5cm,BD=6cm,BC=1cm,点P为直线l上一点,则PA+PD的最小值为 cm;(2)若点A在直线l上向左运动,线段BD在直线l上向右运动,M,N分别为AC,BD的中点(如图2),请指出在此过程中线段AD,BC,MN有何数量关系并说明理由;
(3)若C是AD的一个三等分点,DC>AC,且AD=9cm,E,F两点同时从C,D出发,分别以2cm/s,1cm/s的速度沿直线l向左运动,Q为EF的中点,设运动时间为t,当AQ+AE+AF=![]() AD时,请直接写出t的值.
AD时,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
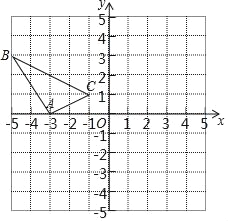
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
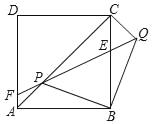
【题目】如图,正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上(点P与A、C不重合),QP与BC交于E,QP延长线与AD交于点F,连接CQ.
(1)①求证:AP=CQ;②求证:PA2=AFAD;
(2)若AP:PC=1:3,求tan∠CBQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
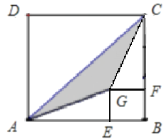
【题目】如图,正方形ABCD与正方形BFGE中,点E在边AB上,若AE=a,BE=b,(其中a>2b).
(1)请用含有a,b的代数式表示图中阴影部分的面积;
(2)当a=5cm,b=3cm时,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小学的时候我们已经学过分数的加减法法则:“同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,转化为同分母分数,再加减.”如:![]() ,反之,这个式子仍然成立,即:
,反之,这个式子仍然成立,即:![]() .
.
(1)问题发现
观察下列等式:
①![]() ,
,
②![]() ,
,
③![]() ,…,
,…,
猜想并写出第![]() 个式子的结果:
个式子的结果:![]() .(直接写出结果,不说明理由)
.(直接写出结果,不说明理由)
(2)类比探究
将(1)中的的三个等式左右两边分别相加得:
![]() ,
,
类比该问题的做法,请直接写出下列各式的结果:
①![]() ;
;
②![]() ;
;
(3)拓展延伸
计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品 | B种产品 | |
成本(万元/件) | 2 | 5 |
利润(万元/件) | 1 | 3 |
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点 A,B,C 分别表示有理数 a,b,c,且![]() , |c-a|=3,点 B,C 表示互为相反数的两个数.
, |c-a|=3,点 B,C 表示互为相反数的两个数.
(1)求点 B,C 表示的数;
(2)计算![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为九年级数学竞赛获奖选手购买以下三种奖品,其中小笔记本每本5元,大笔记本每本7元,钢笔每支10元,购买的大笔记本的数量是钢笔数量的2倍,共花费346元,若使购买的奖品总数最多,则这三种奖品的购买数量各为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com