
【题目】为了进一步了解义务教育阶段学生的体质健康状况,某县从全县九年级学生中随机抽取了部分学生进行了体质抽测.体质抽测的结果分为四个等级:A级:优秀;B级:良好;C级:合格;D级:不合格.并根据抽测结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:(1)本次抽测的学生人数是 人;
(2)图(1)中∠α的度数是 ,并把图(2)条形统计图补充完整;
(3)该县九年级有学生4800名,如果全部参加这次体质测试,请估计不合格的人数为 .
(4)测试老师想从4位同学(分别记为E、F、G、H,其中H为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.
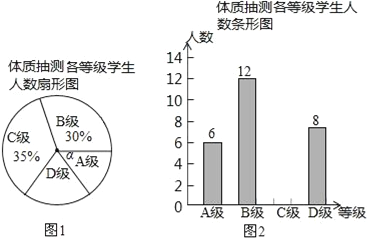
【答案】(1)本次抽样测试的学生人数是40人;
(2)∠α的度数是54°,补图见解析;
(3)不合格有960人;
(4)根据题意画树形图见解析,P(选中小明)= ![]()
【解析】试题分析:(1)用B级的人数除以所占的百分比求出总人数;
(2)用360°乘以A级所占的百分比求出∠α的度数,再用总人数减去A、B、D级的人数,求出C级的人数,从而补全统计图;
(3)用九年级所有得学生数乘以不及格的人数所占的百分比,求出不及格的人数;
(4)根据题意画出树状图,再根据概率公式进行计算即可.
试题解析:
解:(1)本次抽样测试的学生人数是40人,
(2)图1中∠α的度数是54°;
C级的人数是:40-6-12-8=14(人),补图如下:
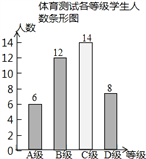
(3)960人;
(4) 将四位同学分别记为E. F.G、H,其中E为小明,根据题意画树形图如下:
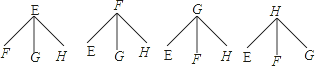
共有12种情况,选中小明的有6种,
则P(选中小明)= ![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E是边AB上一点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连结OM、ON、BM、BN.
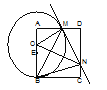
求证:(1)△AOM∽△DMN; (2)求∠MBN的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一粒芝麻约有0.000002千克,0.000002用科学记数学法表示为( )千克.
A.2×10﹣4
B.0.2×10﹣5
C.2×10﹣7
D.2×10﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1 , y2(千米)与行驶时间x(小时)之间的函数关系图象.
(1)填空:A,B两地相距千米;
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)客、货两车何时相遇?相遇处离C站的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动,测量一建筑物CD的高度,他们站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走20m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知观测员的眼睛与地面距离为1.5m(即AB=1.5m),求这栋建筑物CD的高度.(参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414.结果保留整数)
≈1.414.结果保留整数)
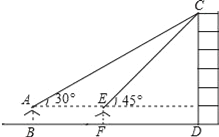
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师出示了问题1:如图1,四边形ABCD是正方形,BC=1,对角线交点记作O,点E是边BC延长线上一点.连接OE交CD边于F,设CE=x,CF=y,求y关于x的函数解析式及其定义域.
(1)经过思考,小明认为可以通过添加辅助线﹣﹣过点O作OM⊥BC,垂足为M求解.你认为这个想法可行吗?请写出问题1的答案及相应的推导过程;
(2)如果将问题1中的条件“四边形ABCD是正方形,BC=1”改为“四边形ABCD是平行四边形,BC=3,CD=2,”其余条件不变(如图2),请直接写出条件改变后的函数解析式;
(3)如果将问题1中的条件“四边形ABCD是正方形,BC=1”进一步改为:“四边形ABCD是梯形,AD∥BC,BC=a,CD=b,AD=c(其中a,b,c为常量)”其余条件不变(如图3),请你写出条件再次改变后y关于x的函数解析式以及相应的推导过程.
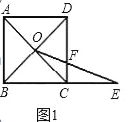
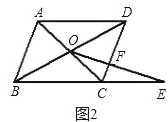
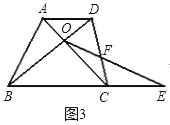
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司准备投资开发A、B两种新产品,信息部通过调研得到两条信息:
信息一:如果投资A种产品,所获利润![]() (万元)与投资金额x(万元)之间满足正比例函数关系:
(万元)与投资金额x(万元)之间满足正比例函数关系: ![]() ;
;
信息二:如果投资B种产品,所获利润![]() (万元)与投资金额x(万元)之间满足二次函数关系:
(万元)与投资金额x(万元)之间满足二次函数关系: ![]() ;
;
根据公司信息部报告, ![]() 、
、![]() (万元)与投资金额x(万元)的部分对应值如下表所示:
(万元)与投资金额x(万元)的部分对应值如下表所示:
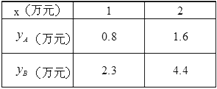
(1)填空: ![]() = ;
= ; ![]() = ;
= ;
(2)如果公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为W(万元),B种产品的投资金额为x(万元),则A种产品的投资金额为_________万元,并求出W与x之间的函数关系式;
(3)请你设计一个在(2)中公司能获得最大总利润的投资方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com