
【题目】用一段长为28m的铁丝网与一面长为8m的墙面围成一个矩形菜园,为了使菜园面积尽可能的大,给出了甲、乙两种围法,请通过计算来说明这个菜园长、宽各为多少时,面积最大?最大面积是多少?
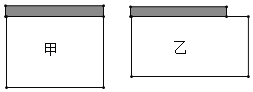
【答案】当矩形的长、宽分别为9m、9m时,面积最大,最大面积为81m2.
【解析】
根据矩形的面积公式甲图列出算式可以直接求面积,乙图设垂直于墙的一边为x,则另一边为(18﹣x)(包括墙长)列出二次函数解析式即可求解.
解:如图甲:设矩形的面积为S,
则S=8×![]() (28﹣8)=80.
(28﹣8)=80.
所以当菜园的长、宽分别为10m、8m时,面积为80;
如图乙:设垂直于墙的一边长为xm,则另一边为![]() (28﹣2x﹣8)+8=(18﹣x)m.
(28﹣2x﹣8)+8=(18﹣x)m.
所以S=x(18﹣x)=﹣x2+18x=﹣(x﹣9)2+81
因为﹣1<0,
当x=9时,S有最大值为81,
所以当矩形的长、宽分别为9m、9m时,面积最大,最大面积为81m2.
综上:当矩形的长、宽分别为9m、9m时,面积最大,最大面积为81m2.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是线段OB上的一点(不与点B重合),D,E是半圆上的点且CD与BE交于点F,用①![]() ,②DC⊥AB,③FB=FD中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
,②DC⊥AB,③FB=FD中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
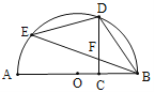
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把分别标有数字1,2,3,4的四个小球放入A袋内,把分别标有数字-1,-2,-2,-3,5的五个小球放入B袋内,所有的小球除了标有的数字不同外,其余完全相同.
(1)学生甲从A、B两个袋子中各摸出一个小球,求这两个小球上的数字互为相反数的概率.
(2)当B袋中标有5的小球的数字变为 时,(1)中的概率为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=a![]() -4ax与x轴交于A,B两点(A在B的左侧).
-4ax与x轴交于A,B两点(A在B的左侧).
(1)求点A,B的坐标;
(2)已知点C(2,1),P(1,-![]() a),点Q在直线PC上,且Q点的横坐标为4.
a),点Q在直线PC上,且Q点的横坐标为4.
①求Q点的纵坐标(用含a的式子表示);
②若抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c(a≠0)与x轴交与A(1,0),B(﹣4,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上求出Q点的坐标使得△QAC的周长最小.
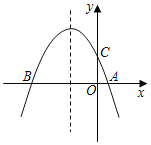
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是二次函数![]() 图象的一部分,对称轴是直线
图象的一部分,对称轴是直线![]() ,与
,与![]() 轴的交点是(0,3),则下列结论中正确的是( )
轴的交点是(0,3),则下列结论中正确的是( )
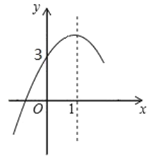
A.![]() ;B.
;B.![]() >0;C.当0<
>0;C.当0<![]() <2时,
<2时,![]() >3;D.关于
>3;D.关于![]() 的方程
的方程![]() 有两个相等的实数根
有两个相等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
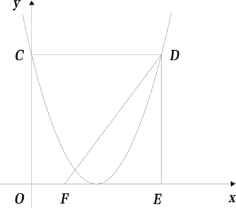
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于点C,过点C作CD∥
轴交于点C,过点C作CD∥![]() 轴交该函数的图象于点D,过点D作DE∥
轴交该函数的图象于点D,过点D作DE∥![]() 轴交
轴交![]() 轴于点E,已知点F(1,0),连接DF.
轴于点E,已知点F(1,0),连接DF.
(1)请求出该函数图象的项点坐标(用含![]() 的代数式表示);
的代数式表示);
(2)如图,若该二次函数的图象的顶点落在![]() 轴上,P为对称轴右侧抛物线上一点;
轴上,P为对称轴右侧抛物线上一点;
①连接PD、PE、PF,若![]() ,求点P的坐标;
,求点P的坐标;
②若∠PFD=![]() ∠DEF,点P的横坐标为m,则m的值为 .
∠DEF,点P的横坐标为m,则m的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
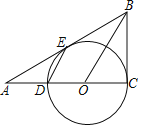
【题目】如图,点D、O在△ABC的边AC上,以CD为直径的⊙O与边AB相切于点E,连结DE、OB,且DE∥OB.
(1)求证:BC是⊙O的切线.
(2)设OB与⊙O交于点F,连结EF,若AD=OD,DE=4,求弦EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
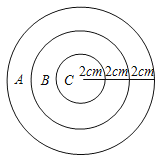
【题目】如图为一个封闭的圆形装置,整个装置内部为A、B、C三个区域(A、B两区域为圆环,C区域为小圆),具体数据如图.
(1)求出A、B、C三个区域三个区域的面积:SA= ,SB= ,SC= ;
(2)随机往装置内扔一粒豆子,多次重复试验,豆子落在B区域的概率PB为多少?
(3)随机往装置内扔180粒豆子,请问大约有多少粒豆子落在A区域?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com