
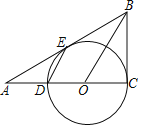
【题目】如图,点D、O在△ABC的边AC上,以CD为直径的⊙O与边AB相切于点E,连结DE、OB,且DE∥OB.
(1)求证:BC是⊙O的切线.
(2)设OB与⊙O交于点F,连结EF,若AD=OD,DE=4,求弦EF的长.
【答案】(1)见解析;(2)4
【解析】
(1)连接OE,根据切线的性质得到OE⊥AB,根据平行线的性质得到∠BOC=∠EDO,∠BOE=∠DEO,根据全等三角形的性质得到∠OCB=∠OEB=90°,于是得到BC是⊙O的切线;
(2)根据直角三角形的性质得到OD=DE=4,推出四边形DOFE是平行四边形,得到EF=OD=4.
(1)证明:连接OE,
∵以CD为直径的⊙O与边AB相切于点E,
∴OE⊥AB,
∵DE∥OB,
∴∠BOC=∠EDO,∠BOE=∠DEO,
∵OE=OD,
∴∠EDO=∠DEO,
∴∠BOC=∠BOE,
∵OB=OB,OC=OE,
∴△OCB≌△OEB(SAS),
∴∠OCB=∠OEB=90°,
∴BC是⊙O的切线;
(2)解:∵∠AEO=90°,AD=OD,
∴ED=![]() AO=OD,
AO=OD,
∴OD=DE=4,
∵DE∥OF,DE=OD=OF,
∴四边形DOFE是平行四边形,
∴EF=OD=4,
∴弦EF的长为4.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
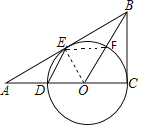
【题目】如图,AB是半圆O的直径,AC是半圆内一条弦,点D是![]() 的中点,DB交AC于点G,过点A作半圆的切线与BD的延长线交于点M,连接AD.点E是AB上的一动点,DE与AC相交于点F.
的中点,DB交AC于点G,过点A作半圆的切线与BD的延长线交于点M,连接AD.点E是AB上的一动点,DE与AC相交于点F.
(1)求证:MD=GD;
(2)填空:①当∠DEA= 时,AF=FG;
②若∠ABD=30°,当∠DEA= 时,四边形DEBC是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代重要建筑的室内上方,通常会在正中部位做出向上凸起的穹窿状装饰,称为藻井.北京故宫博物院内的太和殿上方即有藻井(图1),全称为龙凤角蝉云龙随瓣枋套方八角浑金蟠龙藻井.它展示出精美的装饰空间和造型艺术.从分层构造上来看,太和殿藻井由三层组成:最下层为方井,中层为八角井,上层为圆井.图2是由图1抽象出的平面图形.若最下层方井边长为1,在图2中随机取一点,则此点取自圆内的概率为( )

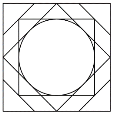
图1 图2
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 小明和同学们对居住在“幸福小区”的部分居民每周户外锻炼天数情况进行了调查,并将调查的居民每周户外锻炼的天数按四个类别进行了统计.四个类别分别是A(每周锻炼少于5天),B(每周锻炼5天),C(每周锻炼6天),D(每周锻炼7天),小明和同学们将统计结果绘制成了如图两幅不完整的统计图.
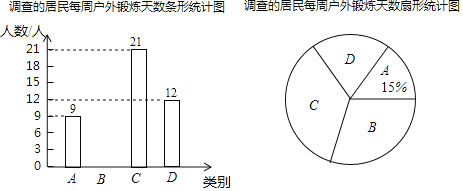
(1)调查的总人数为 人;
(2)扇形统计图中C部分所对应的圆心角的度数为 °;
(3)求类别B的人数,并补全条形统计图;
(4)如果“幸福小区”共有1200名居民,请你估计该小区每周锻炼7天的人数有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过点(﹣1,0),对称轴是x=1,现有结论:①abc>0 ②9a﹣3b+c=0 ③b=﹣2a④(![]() ﹣1)b+c<0,其中正确的有( )
﹣1)b+c<0,其中正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
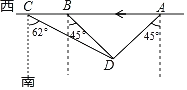
【题目】如图,某海监船向正西方向航行,在A处望见一艘正在作业的渔船D在南偏西45°方向,海监船航行到B处时,望见渔船D在南偏东45°方向,又航行半小时到达C处望见渔船D在南偏东62°方向,若海监船的速度为40海里/小时,求A、B之间的距离.(精确到0.1海里,参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
查看答案和解析>>
科目:初中数学 来源: 题型:
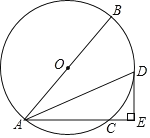
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙ O的切线.
(2)求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com