
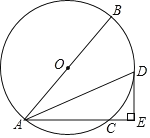
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙ O的切线.
(2)求AD的长.
【答案】(1)证明见解析;(2)AD=4![]() .
.
【解析】
(1)连接OD,欲证明DE是⊙O的切线,只要证明OD⊥DE即可.
(2)过点O作OF⊥AC于点F,只要证明四边形OFED是矩形即可得到DE=OF,在RT△AOF中利用勾股定理求出OF即可.
(1)如图,连接OD.
∵AD平分∠BAC,∴∠DAE=∠DAB.
∵OA=OD,∴∠ODA=∠DAO,∴∠ODA=∠DAE,∴OD∥AE.
∵DE⊥AC,∴OD⊥DE,
∵OD是⊙O的半径,
∴DE是⊙O切线;
(2)过点O作OF⊥AC于点F,∴AF=CF=3,∴OF![]() ,
,
∵∠OFE=∠DEF=∠ODE=90°,∴四边形OFED是矩形,∴DE=OF=4,∴AE=AF+EF=3+5=8
在Rt△ADE中,AD2=DE2+AE2=42+82=80,
∴AD=4![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
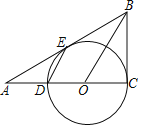
【题目】如图,点D、O在△ABC的边AC上,以CD为直径的⊙O与边AB相切于点E,连结DE、OB,且DE∥OB.
(1)求证:BC是⊙O的切线.
(2)设OB与⊙O交于点F,连结EF,若AD=OD,DE=4,求弦EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆70华诞期间,各超市购物市民络绎不绝,呈现浓浓节日气氛.“百姓超市”用320元购进一批葡萄,上市后很快脱销,该超市又用680元购进第二批葡萄,所购数量是第一批购进数量的2倍,但进价每市斤多了0.2元.
(1)该超市第一批购进这种葡萄多少市斤?
(2)如果这两次购进的葡萄售价相同,且全部售完后总利润不低于![]() ,那么每市斤葡萄的售价应该至少定为多少元?
,那么每市斤葡萄的售价应该至少定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
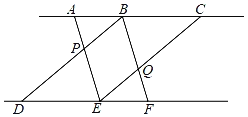
【题目】如图,已知AC∥DF,点B在AC上,点E在DF上,连结AE,BD相交于点P,连结CE,BF相交于点Q,若AB=EF,BC=DE.
(1)求证:四边形BPEQ为平行四边形;
(2)若DP=2BP,BF=3,CE=6.求证:四边形BPEQ为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
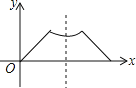
【题目】已知点P为某个封闭图形边界上的一定点,动点M从点P出发,沿其边界顺时针匀速运动一周,设点M的运动时间为x,线段PM的长度为y,表示y与x的函数图象大致如图所示,则该封闭图形可能是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金秋时节,硕果飘香,某精准扶贫项目果园上市一种有机生态水果.为帮助果园拓宽销路,欣欣超市对这种水果进行代销,进价为5元/千克,售价为6元/千克时,当天的销售量为100千克;在销售过程中发现:销售单价每上涨0.5元,当天的销售量就减少5千克.设当天销售单价统一为x元/千克(x≥6,且x是按0.5元的倍数上涨),当天销售利润为y元.
(1)求y与x的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若该种水果每千克的利润不超过80%,要想当天获得利润最大,每千克售价为多少元?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
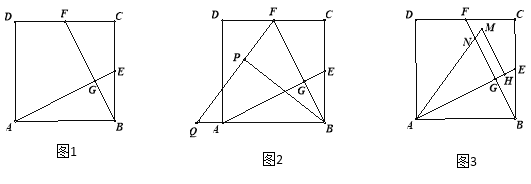
【题目】如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
(1)求证:AE⊥BF;
(2)将△BCF沿BF对折,得到△BPF(如图2),延长FP交BA的延长线于点Q,求sin∠BQP的值;
(3)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,当正方形ABCD的边长为4时,直接写出四边形GHMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
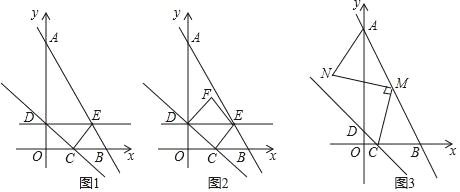
【题目】已知,A(0,8),B(4,0),直线y=﹣x沿x轴作平移运动,平移时交OA于D,交OB于C.
(1)当直线y=﹣x从点O出发以1单位长度/s的速度匀速沿x轴正方向平移,平移到达点B时结束运动,过点D作DE⊥y轴交AB于点E,连接CE,设运动时间为t(s).
①是否存在t值,使得△CDE是以CD为腰的等腰三角形?如果能,请直接写出相应的t值;如果不能,请说明理由.
②将△CDE沿DE翻折后得到△FDE,设△EDF与△ADE重叠部分的面积为y(单位长度的平方).求y关于t的函数关系式及相应的t的取值范围;
(2)若点M是AB的中点,将MC绕点M顺时针旋转90°得到MN,连接AN,请直接写出AN+MN的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com