
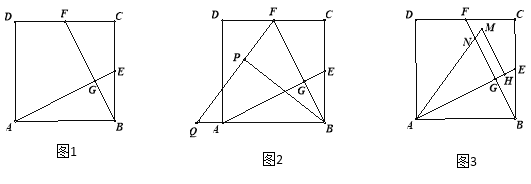
����Ŀ����ͼ1����������ABCD�У�E��F�ֱ�ΪBC��CD���е㣬����AE��BF������ΪG��
(1)��֤��AE��BF��
(2)����BCF��BF���ۣ��õ���BPF����ͼ2�����ӳ�FP��BA���ӳ����ڵ�Q����sin��BQP��ֵ��
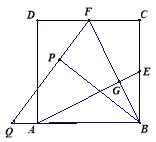
(3)����ABE�Ƶ�A��ʱ�뷽����ת��ʹ��AB��������AE�ϣ��õ���AHM����ͼ3������AM��BF�ཻ�ڵ�N����������ABCD���߳�Ϊ4ʱ��ֱ��д���ı���GHMN�������
���𰸡���1��֤����������2��![]() ��3��
��3��![]()
��������
�����������1������Rt��ABE��Rt��BCF�������ýǵĹ�ϵ�����BGE=90����֤��
��2����BCF��BF���ۣ��õ���BPF�����ýǵĹ�ϵ���QF=QB�����BP��QP��⣻
��3������������εı߳����ٸ�������ȵ������Ʊ߳��ȵ�ƽ�������S��AGN=![]() ��������S�ı���GHMN=S��AHM-S��AGN��⣮
��������S�ı���GHMN=S��AHM-S��AGN��⣮
���������(1)��E��F�ֱ���������ABCD��BC��CD���е㣬
��CF=BE��
��Rt��ABE��Rt��BCF ���BAE=��CBF
���ߡ�BAE+��BEA=900�����CBF+��BEA=900��
���BGE=900�� ��AE��BF
(2)��������ã�FP=FC����PFB=��BFC����FPB=900��
��CD��AB, ���CFB=��ABF��
���ABF=��PFB����QF=QB
��PF=k��k>O������PB=2k��
��Rt��BPQ����QB=x�� ��x2=(x��k)2+4k2, ��x=![]() k��
k��
��sin��BQP=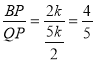
(3) �ı���GHMN�������![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A. ��x+2��2=x2+4 B. ��x-1����-1-x��=x2-1
C. ��-2x+1��2=4x2+4x+1 D. ��x-1����x-2��=x2-3x+2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����ĵ���ͼ�κ���֮���Ӧ�ĵ�ʽ��̽�����еĹ��ɣ�
(1)�����ڢܺ͢ݺ���ĺ����Ϸֱ�д�����Ӧ�ĵ�ʽ��
�١�4��0��1��4��1��3��
��![]() 4��1��1��4��2��3��
4��1��1��4��2��3��
��![]() 4��2��1��4��3��3��
4��2��1��4��3��3��
��![]() ______________��
______________��
��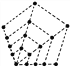 ______________��
______________��
(2)ͨ�����룬д�����![]() ��ͼ�����Ӧ�ĵ�ʽ��
��ͼ�����Ӧ�ĵ�ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=��2x2������ƽ��1����λ��������ƽ��2����λ�����ú�������ʽ�ǣ� ����
A. y=��2��x��1��2+2B. y=��2��x��1��2��2C. y=��2��x+1��2+2D. y=��2��x+1��2��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��ƽ���ı���ABCD�У�����D��![]() �ڵ�E����F�ڱ�CD�ϣ�
�ڵ�E����F�ڱ�CD�ϣ�![]() ������AF��BF��
������AF��BF��
(1)��֤���ı���BFDE�Ǿ��Σ�
(2)��![]() ��
��![]() ��
��![]() ����֤��AFƽ��
����֤��AFƽ��![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ��ʾ����֪��AOB��90������BOC��30����OMƽ�֡�AOC��ONƽ�֡�BOC�����MON�Ķ�����
(2)���(1)�С�AOB�����������������䣬���MON�Ķ�����
(3)���(1)�С�BOC����(��Ϊ���)�������������������MON�Ķ�����
(4)��(1)(2)(3)�Ľ�������ܿ���ʲô���ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й���������һ��һ·�����轫�ٽ��ҹ�����������Ļ�������.���ݹ滮����һ��һ·�������������˿�ԼΪ4400000000�ˣ�������ÿ�ѧ��������ʾΪ (�� ��)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
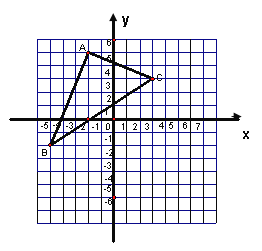
����Ŀ������ABC����ƽ��4����λ���ȣ�������ƽ��5����λ���ȣ�
��1����ͼ�ϻ�����Ӧ��������A1B1C1��
��2�����A1��B1��C1������.
��3�������A1B1C1�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ƽ��ֱ������ϵ�У�ֱ��AB��x�ᣬy��ֱ���A��B�뷴��������![]() ��k>0��Ϊ�������ڵ�һ����ͼ���ڵ�E��F������E��EM��y����M������F��FN��x����N��ֱ��EM��FN���ڵ�C����
��k>0��Ϊ�������ڵ�һ����ͼ���ڵ�E��F������E��EM��y����M������F��FN��x����N��ֱ��EM��FN���ڵ�C����![]() , ��
, ��![]() ____
____

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com