
【题目】 在平行四边形ABCD中,过点D作![]() 于点E,点F在边CD上,
于点E,点F在边CD上,![]() ,连接AF,BF。
,连接AF,BF。
(1)求证:四边形BFDE是矩形;
(2)若![]() ,
,![]() ,
,![]() ,求证:AF平分
,求证:AF平分![]() 。
。

【答案】(1)证明见解析(2)证明见解析
【解析】
试题分析:(1)根据□ABCD的对边互相平行得出DC∥AB,又因为DF=BE,即可得出四边形DEBF是平行四边形,再根据有一个角是直角的平行四边形是矩形得出结论.
(2)在Rt△BFC中,根据勾股定理得出BC=5,又因为AD=BC=5,得出AD=DF,得出∠DAF=∠DFA,再根据AB∥CD,得出∠FAB=∠DFA,等量代换即可.
试题解析:(1)∵四边形ABCD为平行四边形
∴DC∥AB,
即DF∥BE
又∵DF=BE
∴四边形DEBF是平行四边形
又∵DE⊥AB,
即∠DEB=90°
∴四边形DEBF是矩形
(2)∵四边形DEBF是矩形,
∴∠BFC=90°
∵CF=3,BF=4
∴BC=![]() =5
=5
∴AD=BC=5
∴AD=DF=5
∴∠DAF=∠DFA
∵AB∥CD
∴∠FAB=∠DFA
∠FAB=∠DFA
∴AC平分∠DAB


科目:初中数学 来源: 题型:
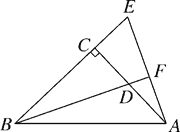
【题目】如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料并解决有关问题:我们知道: 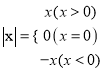 ,现在我们可以用这一结论来化简含有绝对值的式子。
,现在我们可以用这一结论来化简含有绝对值的式子。
如化简代数式|x+1|+|x-2|时,可令x+1=0 或 x-2=0,分别求得x=-1,x=-2(称-1,2分别为|x+1|和|x-2|的零点值。
在有理数范围内,零点值x=-1和x=2,可将全体有理数分成不重复且不遗漏的如下3种情况:(1)<-1;(2)-1![]() x
x![]() (3)x
(3)x![]() -2
-2
|从而化简式子|x+1|+|x-2|可分以下3种情况:
(1)当x<-1时,原式=-(x+1)-(x-2)=-2x+1;
(2)当-1![]() x
x![]() 时,原式= x+1-(x-2) =3;
时,原式= x+1-(x-2) =3;
(3)当x![]() -2时,原式=x+1+(x-2)=2x-1
-2时,原式=x+1+(x-2)=2x-1
综上所述,原式=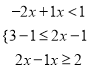
通过以上阅读,请你解决以下问题:“(1)化简|x-4|-|x+2|
(2)|x|+|x+1|+|x+2|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校的一次劳动中,在甲处劳动的有27人,在乙处劳动的有19人,后因劳动任务需要,需要另外调20人来支援,使在甲处的人数是在乙处人数的2倍,则应调往甲_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
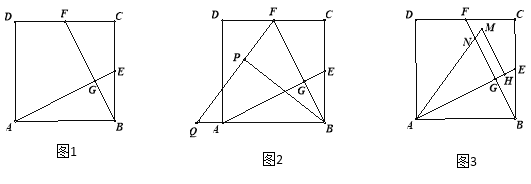
【题目】如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
(1)求证:AE⊥BF;
(2)将△BCF沿BF对折,得到△BPF(如图2),延长FP交BA的延长线于点Q,求sin∠BQP的值;
(3)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,当正方形ABCD的边长为4时,直接写出四边形GHMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,MN,EF是两面互相平行的镜面,根据镜面反射规律,若一束光线AB照射到镜面MN上,反射光线为BC,则一定有∠1=∠2.试根据这一规律:

(1)利用直尺和量角器作出光线BC经镜面EF反射后的反射光线CD;
(2)试判断AB与CD的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com