【题目】函数y=﹣2x2先向右平移1个单位，再向下平移2个单位，所得函数解析式是（ ）
A. y=﹣2（x﹣1）2+2B. y=﹣2（x﹣1）2﹣2C. y=﹣2（x+1）2+2D. y=﹣2（x+1）2﹣2
提分百分百检测卷系列答案科目：初中数学 来源： 题型：
【题目】下列计算结果正确的是（ ）
A.6x6÷2x3＝3x2
B.x2+x2＝x4
C.﹣2x2y（x﹣y）＝﹣2x3y+2x2y2
D.（﹣3xy2）3＝﹣9x3y6
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数y=ax2+bx（a≠0）的图象经过点A（1，4），对称轴是直线x=﹣
，线段AD平行于x轴，交抛物线于点D．在y轴上取一点C（0，2），直线AC交抛物线于点B，连结OA，OB，OD，BD．
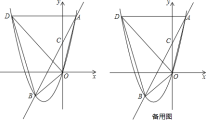
（1）求该二次函数的解析式；
（2）求点B坐标和坐标平面内使△EOD∽△AOB的点E的坐标；
（3）设点F是BD的中点，点P是线段DO上的动点，问PD为何值时，将△BPF沿边PF翻折，使△BPF与△DPF重叠部分的面积是△BDP的面积的
？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料并解决有关问题：我们知道：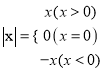 
，现在我们可以用这一结论来化简含有绝对值的式子。
如化简代数式|x+1|+|x-2|时，可令x+1=0 或 x-2=0，分别求得x=-1，x=-2(称-1，2分别为|x+1|和|x-2|的零点值。
在有理数范围内，零点值x=-1和x=2，可将全体有理数分成不重复且不遗漏的如下3种情况：（1）<-1；（2）-1
x
(3)x
-2
|从而化简式子|x+1|+|x-2|可分以下3种情况：
（1）当x<-1时，原式=-（x+1）-（x-2）=-2x+1；
（2）当-1
x
时，原式= x+1-(x-2) =3；
（3）当x
-2时，原式=x+1+(x-2)=2x-1
综上所述，原式=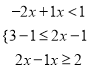
通过以上阅读，请你解决以下问题：“（1）化简|x-4|-|x+2|
(2)|x|+|x+1|+|x+2|
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
小明同学平时爱好数学，他探索发现了：从2开始，连续的几个偶然相加，它们和的情况的变化规律如下：
2=1
2
2+4=2
3
2+4+6=3
4
2+4+6+8=4
5
……
请你根据上述规律解答下列问题：
（1）试一试：2+4+6+8+10+12+14+16= ；
（2）猜一猜：2+4+……+2n= ；（用含n的式子表示）
（3）用一用：利用上题的猜想结果，计算202+204+206+……+498+500的值（要有计算过程）
查看答案和解析>>
科目：初中数学 来源： 题型：
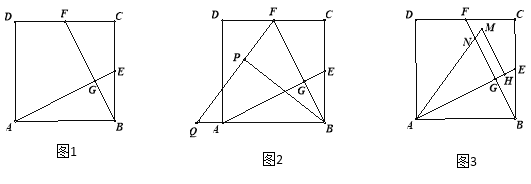
【题目】如图1，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE、BF，交点为G．
(1)求证：AE⊥BF；
(2)将△BCF沿BF对折，得到△BPF（如图2），延长FP交BA的延长线于点Q，求sin∠BQP的值；
(3)将△ABE绕点A逆时针方向旋转，使边AB正好落在AE上，得到△AHM（如图3），若AM和BF相交于点N，当正方形ABCD的边长为4时，直接写出四边形GHMN的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
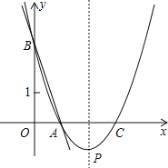
【题目】如图，直线y=-3x+3与x轴、y轴分别交于点A、B，抛物线
经过点A、B，并与x轴交于另一点C，其顶点为P．
（1）求
，
的值；
（2）抛物线的对称轴上有一点Q，使△ABQ是以AB为底边的等腰三角形，求Q点的坐标；
（3）在抛物线及其对称轴上分别取点M、N，使以A，C，M，N为顶点的四边形为正方形，求此正方形的边长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（本题7分）数学课上，探讨角平分线的作法时，李老师用直尺和圆规作角平分线，方法如下：
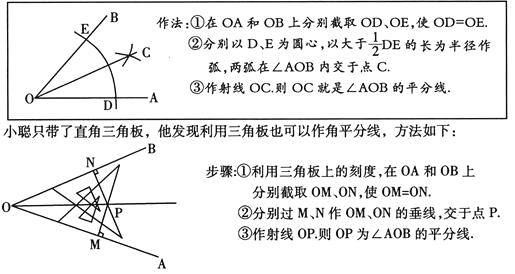
根据以上情境，解决下列问题：
（1）李老师用尺规作角平分线时，用到的三角形全等的判定方法是 ．
（2）小聪的作法正确吗？请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
