
【题目】如图,二次函数y=ax2+bx(a≠0)的图象经过点A(1,4),对称轴是直线x=﹣![]() ,线段AD平行于x轴,交抛物线于点D.在y轴上取一点C(0,2),直线AC交抛物线于点B,连结OA,OB,OD,BD.
,线段AD平行于x轴,交抛物线于点D.在y轴上取一点C(0,2),直线AC交抛物线于点B,连结OA,OB,OD,BD.
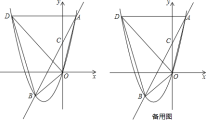
(1)求该二次函数的解析式;
(2)求点B坐标和坐标平面内使△EOD∽△AOB的点E的坐标;
(3)设点F是BD的中点,点P是线段DO上的动点,问PD为何值时,将△BPF沿边PF翻折,使△BPF与△DPF重叠部分的面积是△BDP的面积的![]() ?
?
【答案】(1) y=x2+3x(2)当点E的坐标是(8,﹣2)或(2,﹣8)时,△EOD∽△AOB;(3)PD=![]() 或PD=3
或PD=3![]()
【解析】
试题分析:(1)运用待定系数法和对称轴的关系式求出a、b的即可;
(2)由待定系数法求出直线AC的解析式,由抛物线的解析式构成方程组就可以求出B点的坐标,由相似三角形的性质及旋转的性质就可以得出E的坐标;
(3)分情况讨论当点B落在FD的左下方,点B,D重合,点B落在OD的右上方,由三角形的面积公式和菱形的性质的运用就可以求出结论.
试题解析:1)∵y=ax2+bx(a≠0)的图象经过点A(1,4),且对称轴是直线x=﹣![]() ,
,
∴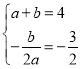 ,
,
解得:![]() ,
,
∴二次函数的解析式为y=x2+3x;
(2)如图1,

∵点A(1,4),线段AD平行于x轴,
∴D的纵坐标为4,
∴4=x2+3x,
∴x1=﹣4,x2=1,
∴D(﹣4,4).
设直线AC的解析式为y=kx+b,由题意,得
![]() ,
,
解得:![]() ,
,
∴y=2x+2;
当2x+2=x2+3x时,
解得:x1=﹣2,x2=1(舍去).
∴y=﹣2.
∴B(﹣2,﹣2).
∴DO=4![]() ,BO=2
,BO=2![]() ,BD=2
,BD=2![]() ,OA=
,OA=![]() .
.
∴DO2=32,BO2=8,BD2=40,
∴BO2+BO2=BD2,
∴△BDO为直角三角形.
∵△EOD∽△AOB,
∴∠EOD=∠AOB,![]() ,
,
∴∠EOD﹣∠AOB=∠AOB﹣∠AOB,
∴∠BOD=∠AOE=90°.
即把△AOB绕着O点顺时针旋转90°,OB落在OD上B′,OA落在OE上A1
∴A1(4,﹣1),
∴E(8,﹣2).
作△AOB关于x轴的对称图形,所得点E的坐标为(2,﹣8).
∴当点E的坐标是(8,﹣2)或(2,﹣8)时,△EOD∽△AOB;
(3)由(2)知DO=4![]() ,BO=2
,BO=2![]() ,BD=2
,BD=2![]() ,∠BOD=90°.
,∠BOD=90°.
若翻折后,点B落在FD的左下方,如图2.

S△HFP=![]() S△BDP=
S△BDP=![]() S△DPF=
S△DPF=![]() S△B′PF=S△DHP=S△B′HF,
S△B′PF=S△DHP=S△B′HF,
∴DH=HF,B′H=PH,
∴在平行四边形B′FPD中,PD=B′F=BF=![]() BD=
BD=![]() ;
;
若翻折后,点B,D重合,S△HFP=![]() S△BDP,不合题意,舍去.
S△BDP,不合题意,舍去.
若翻折后,点B落在OD的右上方,如图3,

S△HFP=![]() S△BDP=
S△BDP=![]() S△BPF=
S△BPF=![]() S△DPF=
S△DPF=![]() S△B′PF=S△DHF=S△B′HP
S△B′PF=S△DHF=S△B′HP
∴B′P=BP,B′F=BF.DH=HP,B′H=HF,
∴四边形DFPB′是平行四边形,
∴B′P=DF=BF,
∴B′P=BP=B′F=BF,
∴四边形B′FPD是菱形,
∴FD=B′P=BP=![]() BD=
BD=![]() ,根据勾股定理,得
,根据勾股定理,得
OP2+OB2=BP2,
∴(4![]() ﹣PD)2+(2
﹣PD)2+(2![]() )2=(
)2=(![]() )2,
)2,
PD=3![]() ,PD=5
,PD=5![]() >4
>4![]() (舍去),
(舍去),
综上所述,PD=![]() 或PD=3
或PD=3![]() 时,将△BPF沿边PF翻折,使△BPF与△DPF重叠部分的面积是△BDP的面积的
时,将△BPF沿边PF翻折,使△BPF与△DPF重叠部分的面积是△BDP的面积的![]() .
.


科目:初中数学 来源: 题型:
【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间 x(单位:h)变化的图象如图所示,

根据图中提供的信息,有下列说法:①两人相遇前,甲的速度小于乙的速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的有____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)一个多边形的内角和是外角和的2倍,它是几边形?
(2)如图所示,在△ABC中,AB=AC,AC边上的中线把三角形的周长分为24 cm和30 cm的两部分,求三角形各边的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知, A、B、C、D、E是反比例函数![]() (x>0)上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图5所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是 (用含π的代数式表示)
(x>0)上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图5所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是 (用含π的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面的点阵图形和与之相对应的等式,探究其中的规律:
(1)请你在④和⑤后面的横线上分别写出相对应的等式.
①·4×0+1=4×1-3;
②![]() 4×1+1=4×2-3;
4×1+1=4×2-3;
③![]() 4×2+1=4×3-3;
4×2+1=4×3-3;
④![]() ______________;
______________;
⑤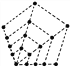 ______________;
______________;
(2)通过猜想,写出与第![]() 个图形相对应的等式.
个图形相对应的等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=﹣2x2先向右平移1个单位,再向下平移2个单位,所得函数解析式是( )
A. y=﹣2(x﹣1)2+2B. y=﹣2(x﹣1)2﹣2C. y=﹣2(x+1)2+2D. y=﹣2(x+1)2﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果中你能看出什么规律?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店欲购进甲、乙两种商品,已知甲的进价是乙的进价的一半,进3件甲商品和1件乙商品恰好用200元.甲、乙两种商品的售价每件分别为80元、130元,该商店决定用不少于6710元且不超过6810元购进这两种商品共100件.
(1)求这两种商品的进价;
(2)该商店有几种进货方案?哪种进货方案可获得最大利润,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com