练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在20km越野赛中，甲乙两选手的行程y（单位：km）随时间 x（单位：h）变化的图象如图所示，

    根据图中提供的信息，有下列说法：①两人相遇前，甲的速度小于乙的速度；②出发后1小时，两人行程均为10km；③出发后1.5小时，甲的行程比乙多3km；④甲比乙先到达终点．其中正确的有____个．

    【答案】3

    【解析】试题解析：在两人出发后0.5小时之前，甲的速度小于乙的速度，0.5小时到1小时之间，甲的速度大于乙的速度，故①错误；

    由图可得，两人在1小时时相遇，行程均为10km，故②正确；

    甲的图象的解析式为y=10x，乙AB段图象的解析式为y=4x+6，因此出发1.5小时后，甲的路程为15千米，乙的路程为12千米，甲的行程比乙多3千米，故③正确；

    甲到达终点所用的时间较少，因此甲比乙先到达终点，故④正确．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，E、F分别是□ABCD的边BC、AD上的中点.

    （1） 求证：△ABE≌△CDF；

    （2） 当∠BAC= ° 时，四边形AECF是菱形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校学生会为了解该校学生喜欢球类活动的情况，采取抽样调查的办法，从足球、乒乓球、篮球、排球等四个方面调查了若干名学生的兴趣爱好，并将调查的结果绘制成右边的两幅不完整的统计图（如图（1），图（2），要求每位同学只能选择一种自己喜欢的球类；图中用乒乓球、足球、排球、篮球代表喜欢这四种球类中的某一种球类的学生人数），请你根据图中提供的信息，解答下列问题：

    （1）在这次研究中，一共调查了多少名学生？

    （2）喜欢排球的人数在扇形统计图中所占的圆心角是多少度？

    （3）补全频数分布折线统计图.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，△ABC中，∠BAC=90°，AB=AC，AE是过A点的一条直线，且B、C在AE的异侧，BD⊥AE于D，CE⊥AE于E，求证：BD=DE+CE．

    （2）若直线AE绕点A旋转到图2的位置时（BD＜CE），其余条件不变，问BD与DE、CE的关系如何？请予以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

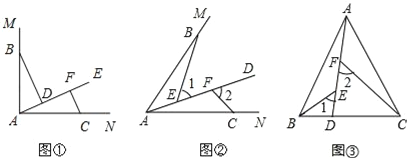
    【题目】（1）如图1，∠MAN=90°，射线AE在这个角的内部，点B、C分别在∠MAN的边AM、AN上，且AB=AC，CF⊥AE于点F，BD⊥AE于点D．求证：△ABD≌△CAF；

    （2）如图2，点B、C分别在∠MAN的边AM、AN上，点E、F都在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，且∠1=∠2=∠BAC．求证：△ABE≌△CAF；

    （3）如图3，在△ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为15，求△ACF与△BDE的面积之和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为增强公民节水意识，合理利用水资源，某市采用“阶梯收费”，标准如下表：

    用水量

    单价

    不超过6m3 的部分

    2元/ m3

    超过6m3不超过10m3的部分

    4元/m3

    超出10m3的部分

    8元/m3

    譬如：某用户2月份用水9m3，则应缴水费：2×6+4×(9－6)=24(元)

    (1)某用户3月用水15 m3应缴水费多少元？

    (2) 已知某用户4月份缴水费20元，求该用户4月份的用水量；

    (3) 如果该用户5、6月份共用水20m3 （6月份用水量超过5月份用水量），共交水费64元，则该户居民5、6月份各用水多少立方米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算结果正确的是（　　）

    A.6x6÷2x3＝3x2

    B.x2+x2＝x4

    C.﹣2x2y（x﹣y）＝﹣2x3y+2x2y2

    D.（﹣3xy2）3＝﹣9x3y6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】方程x2+3x+1=0的根的情况是： ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数y=ax2+bx（a≠0）的图象经过点A（1，4），对称轴是直线x=﹣，线段AD平行于x轴，交抛物线于点D．在y轴上取一点C（0，2），直线AC交抛物线于点B，连结OA，OB，OD，BD．

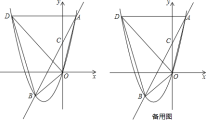
    （1）求该二次函数的解析式；

    （2）求点B坐标和坐标平面内使△EOD∽△AOB的点E的坐标；

    （3）设点F是BD的中点，点P是线段DO上的动点，问PD为何值时，将△BPF沿边PF翻折，使△BPF与△DPF重叠部分的面积是△BDP的面积的？

    查看答案和解析>>

    同步练习册答案