
【题目】如图所示,已知O是直线AB上一点,∠BOE=∠FOD=90°,OB平分∠COD
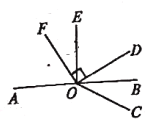
(1)图中与∠DOE互余的角是______________________
(2)图中是否有与∠DOE互补的角?如果有,直接写出全部结果;如果没有,说明理由。
(3)如果∠EOD︰∠EOF=3︰2,求∠AOC的度数
【答案】(1)∠EOF、∠BOD、∠BOC;(2)有,∠BOF和∠EOC;(3)144°
【解析】
(1)由∠BOE=90°,则∠DOE+∠BOD=90°,要求与∠DOE互余的角,只要找到与∠BOD相等的角即可,即∠BOC,∠EOF;
(2)根据同角的余角相等,结合OB平分∠COD,可得∠DOE=∠AOF,∠EOF=∠BOD=∠BOC,则∠DOE的补角与∠AOF的补角相等,即∠DOE互补的角:∠BOF、∠EOC;
(3)由∠EOD︰∠EOF=3︰2,则求出∠EOF=36°,即可得到∠BOC=36°,利用互补关系,即可得到∠AOC的度数.
解:(1)∵∠BOE=∠FOD=90°,
∴∠AOF+∠EOF=90°,∠BOD+∠DOE=90°,∠DOE+∠EOF=90°,
∵OB平分∠COD,
∴∠BOD=∠BOC,∠AOF=∠DOE,
∴与∠DOE互余的是:∠EOF、∠BOD、∠BOC;
故答案为:∠EOF、∠BOD、∠BOC;
(2)由(1)以及同角的余角相等可知,∠AOF=∠DOE,∠EOF=∠BOD=∠BOC,
∴∠DOE的补角与∠AOF的补角相等,
∵∠AOF+∠BOF=180°,∠BOF=∠EOC,
∴∠AOF+∠EOC=180°,
∴∠DOE的补角有:∠BOF和∠EOC;
(3)∵∠EOD︰∠EOF=3︰2,∠DOF=∠EOD+∠EOF=90°,
∴∠EOF=![]() ,
,
∴∠BOC=36°,
∴∠AOC=![]() .
.


科目:初中数学 来源: 题型:
【题目】我市绿化部门决定利用现有的不同种类花卉搭配园艺造型,摆放于城区主要大道的两侧.A、B两种园艺造型均需用到杜鹃花,A种造型每个需用杜鹃花25盆,B种造型每个需用杜鹃花35盆,解答下列问题:
(1)已知人民大道两侧搭配的A、B两种园艺造型共60个,恰好用了1700盆杜鹃花,A、B两种园艺造型各搭配了多少个?
(2)如果搭配一个A种造型的成本W与造型个数![]() 的关系式为:W=100―
的关系式为:W=100―![]() x (0<x<50),搭配一个B种造型的成本为80元.现在观海大道两侧也需搭配A、B两种园艺造型共50个,要求每种园艺造型不得少于20个,并且成本总额y(元)控制在4500元以内. 以上要求能否同时满足?请你通过计算说明理由.
x (0<x<50),搭配一个B种造型的成本为80元.现在观海大道两侧也需搭配A、B两种园艺造型共50个,要求每种园艺造型不得少于20个,并且成本总额y(元)控制在4500元以内. 以上要求能否同时满足?请你通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进货价为35元台灯以50元销售价售出,平均每月能售出500个,市场调研表明:当销售价每上涨1元时,其销售量就将减少10个![]() 若设每个台灯的销售价上涨a元.
若设每个台灯的销售价上涨a元.
![]() 试用含a的代数式填空:涨价后,每个台灯的销售价为______元,利润为______元,商场的台灯平均每月的销售量为______台
试用含a的代数式填空:涨价后,每个台灯的销售价为______元,利润为______元,商场的台灯平均每月的销售量为______台![]()
![]() 如果商场要想销售利润平均每月达到10000,商场经理甲说:“在原售价每台50元的基础上再上涨25元,可以完成任务”,商场经理乙说:“不用涨那么多,在原售价每台50元的基础上再上涨15元就可以了”,为减少库存,应该采取谁的意见?
如果商场要想销售利润平均每月达到10000,商场经理甲说:“在原售价每台50元的基础上再上涨25元,可以完成任务”,商场经理乙说:“不用涨那么多,在原售价每台50元的基础上再上涨15元就可以了”,为减少库存,应该采取谁的意见?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽、小明练习打字,已知小丽比小明每分钟多打80个字,小丽打3500个字的时间与小明打2500个字的时间相同.
(1)小丽、小明每分钟分别可打多少字?
(2)如果有一份总字数为m的稿件需要输入电脑,小丽工作了![]() 个小时后余下的输入工作由小明继续完成,则小明还需要工作多少小时?(所得结果用含有
个小时后余下的输入工作由小明继续完成,则小明还需要工作多少小时?(所得结果用含有![]() 的代数式表示;
的代数式表示;![]() 均为大于零的正数)
均为大于零的正数)
查看答案和解析>>
科目:初中数学 来源: 题型:
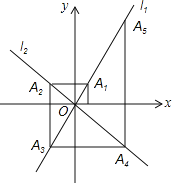
【题目】如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过A1点作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2019的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树AB的高度,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,求树AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:![]() ______ (2)计算:
______ (2)计算:![]() _________
_________
(3)计算:![]() ________ (4)计算:
________ (4)计算:![]() =________
=________
(5)计算:![]() =__________ (6)计算:
=__________ (6)计算:![]() ____________
____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;

(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;

(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
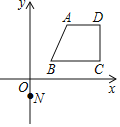
【题目】如图,过点N(0,-1)的直线y=kx+b与图中的四边形ABCD有不少于两个交点,其中A(2,3)、B(1,1)、C(4,1)、D(4,3),则k的取值范围____________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com