
如图1,小红将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=15,AD=12.在进行如下操作时遇到了下面的几个问题,请你帮助解决.

(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2)求FB的长度
(2)在(1)的条件下,小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4,请问哪种包裹纸片的方法使得未包裹住的面积大?(纸片厚度忽略不计)请你通过计算说服小红。

(1)30;(2) 二种包裹纸片的方法使得未包裹住的面积相等.
【解析】
试题分析:(1)利用矩形的性质以及得出△ADE∽△FBE,求出即可;
(2)根据Rt△F,HN~Rt△F,EG,得到HN=3,从而S△AMH=144;由Rt△GBE~Rt△C,B,G,得到GB,=24,从而S△B,C,G=144,进行比较即可.
⑴BE=AD=15,在RtBCE中,CE2=B E2-BC2=152-122,求得CE=9,DE=6,
证Rt△ADE~Rt△FBE,
求得BF=30
⑵①如图1,将矩形ABCD和Rt△FBE以CD为轴翻折,则△AMH即为未包裹住的面积,
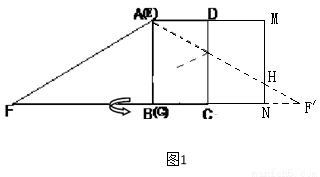
由Rt△F,HN~Rt△F,EG,得到HN=3,
从而S△AMH=144
②如图2,将矩形ABCD和Rt△ECF以AD为轴翻折,由Rt△GBE~Rt△C,B,G,得到GB,=24,
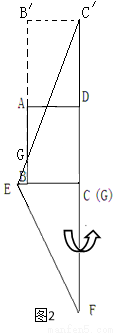
从而S△B,C,G=144,∴未包裹的面积为144.
∴按照二种包裹的方法未包裹的面积相等。
考点:几何变换综合题.


科目:初中数学 来源:2013-2014学年江苏省江阴市九年级下学期期中考试数学试卷(解析版) 题型:填空题
据统计,今年无锡南长区“古运河之光”旅游活动节期间,访问南长历史文化街区的国内外游客约908万人次,908万人次用科学记数法可表示为 人次.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省江阴市九年级下学期期中考试数学试卷(解析版) 题型:选择题
若⊙O1和⊙O2的半径分别为3cm、4cm,圆心距O1O2为5cm,则这两圆位置关系( )
A.内切 B.外切 C.内含 D.相交
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省江阴市九年级一模数学试卷(解析版) 题型:解答题
有两个可以自由转动的均匀转盘A,B都被分成了3等分,并在每一份内均标有数字,如图所示,规则如下: ①分别转动转盘A,B;②两个转盘停止后观察两个指针所指份内的数字(若指针停在等分线上,那么重转一次,直到指针指向某一份内为止).
(1)请用树状图或列表法列出所有可能的结果;
(2)王磊和张浩想用这两个转盘做游戏,他们规定:若“两个指针所指的数字都是方程x2-5x+6=0的解”时,王磊得1分;若“两个指针所指的数字都不是方程x2-5x+6=0的解”时,张浩得3分,这个游戏公平吗?为什么?

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省昆山市九年级下学期教学质量调研(二模)数学试卷(解析版) 题型:解答题
在平面直角坐标系xOy中,已点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过D作OD⊥OC,OD与⊙O相交于点D(其中点C、D按顺时针方向排列),连接AB.
(1)当OC//AB时,∠BOC的度数为
(2)连接AC、BC,当点C在⊙O上运动到什么位置时,△ABC的面积最大?并求出△ABC的面积的最大值.
(3)连接AD,当OC//AD时,
①求出点C的坐标;
②直线BC是否为⊙O的切线?请作出判断,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com