
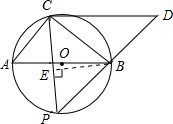
 在半圆弧AB上运动(不与A、B两点重合),过点C作CP的垂线CD交PB的延长线于D点.
在半圆弧AB上运动(不与A、B两点重合),过点C作CP的垂线CD交PB的延长线于D点. 对的圆周角,
对的圆周角,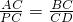 ,
, (2)解:当点P运动到
(2)解:当点P运动到 的中点时,过点B作BE⊥PC于E,
的中点时,过点B作BE⊥PC于E, 的中点,
的中点, ∠ACB=45°,
∠ACB=45°, =4
=4 ,
,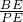 =
= =
= ,
, BE=3
BE=3 ,
, ,
, ×7
×7 =
=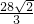 .
. 对的圆周角,由圆周角定理,可得∠A=∠P,即可判定△ABC∽△PDC,又由相似三角形的对应边成比例,求得答案;
对的圆周角,由圆周角定理,可得∠A=∠P,即可判定△ABC∽△PDC,又由相似三角形的对应边成比例,求得答案; 的中点,可得∠PCB=
的中点,可得∠PCB= ∠ACB=45°,然后利用三角函数的性质,求得BE,CE的长,继而求得PE,CD的长.
∠ACB=45°,然后利用三角函数的性质,求得BE,CE的长,继而求得PE,CD的长.

 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
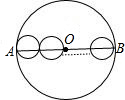 如图,⊙O的直径为AB,周长为P1,在⊙O内的n个圆心在AB上且依次相外切的等圆,且其中左、右两侧的等圆分别与⊙O内切于A、B,若这n个等圆的周长之和为P2,则P1和P2的大小关系是( )
如图,⊙O的直径为AB,周长为P1,在⊙O内的n个圆心在AB上且依次相外切的等圆,且其中左、右两侧的等圆分别与⊙O内切于A、B,若这n个等圆的周长之和为P2,则P1和P2的大小关系是( )| A、P1<P2 | B、P1=P2 | C、P1>P2 | D、不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
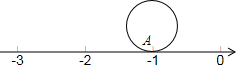 如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是
如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com