
【题目】任何一个正整数n都可以进行这样的分解:n=s×t(s,t是正整数,且s≤t),如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:![]() 、例如18可以分解成1×18,2×9,3×6这三种,这时就有
、例如18可以分解成1×18,2×9,3×6这三种,这时就有![]() .给出下列关于F(n)的说法:(1)
.给出下列关于F(n)的说法:(1)![]() ;(2)
;(2)![]() ;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____.
;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____.
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各多少万元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元. 则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为:;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.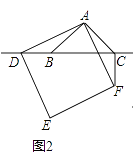
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2 ![]() ,CD=
,CD= ![]() BC,请求出GE的长.
BC,请求出GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解决提出的问题:
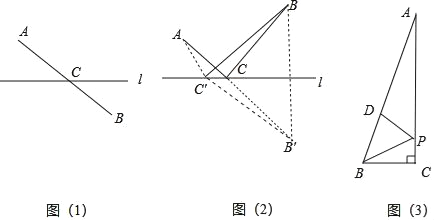
最短路径问题:如图(1),点A,B分别是直线l异侧的两个点,如何在直线l上找到一个点C,使得点C到点A,点B的距离和最短?我们只需连接AB,与直线l相交于一点,可知这个交点即为所求.
如图(2),如果点A,B分别是直线l同侧的两个点,如何在l上找到一个点C,使得这个点到点A、点B的距离和最短?我们可以利用轴对称的性质,作出点B关于的对称点B,这时对于直线l上的任一点C,都保持CB=CB,从而把问题(2)变为问题(1).因此,线段AB与直线l的交点C的位置即为所求.
为了说明点C的位置即为所求,我们不妨在直线上另外任取一点C′,连接AC′,BC′,B′C′.因为AB′≤AC′+C′B′,∴AC+CB<AC'+C′B,即AC+BC最小.
任务:
数学思考
(1)材料中划线部分的依据是 .
(2)材料中解决图(2)所示问题体现的数学思想是 .(填字母代号即可)
A.转化思想
B.分类讨论思想
C.整体思想
迁移应用
(3)如图,在Rt△ABC中,∠C=90°,∠BAC=15°,点P为C边上的动点,点D为AB边上的动点,若AB=8cm,则BP+DP的最小值为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市先后两次共进货板栗![]() ,进货价依次为10元
,进货价依次为10元![]() 和8元
和8元![]() ,且第二次比第一次多付款800元.
,且第二次比第一次多付款800元.
(1)该超市这两次购进的板栗分别是多少吨?
(2)超市对这![]() 板栗以14元
板栗以14元![]() 的标价销售了
的标价销售了![]() 后,把剩下的板栗全部打折售出,合计获得利润4570元,问超市对剩下的板栗打几折销售?(利润=销售总收入-进货总成本)
后,把剩下的板栗全部打折售出,合计获得利润4570元,问超市对剩下的板栗打几折销售?(利润=销售总收入-进货总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李师傅负责修理我校课桌椅,现知道李师傅修理2张课桌和3把椅子共需86分钟,修理5张课桌和2把椅子共需149分钟.
(1)请问李师傅修理1张课桌和1把椅子各需多少分钟
(2)现我校有12张课桌和14把椅子需要修理,要求1天做完,李师傅每天工作8小时,请问李师傅能在上班时间内修完吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连结CQ.若PA∶PB∶PC=3∶4∶5,连结PQ,试判断△PQC的形状( )

A. 直角三角形 B. 等腰三角形 C. 锐角三角形 D. 钝角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个由若干小正方形堆成的几何体,它从正面看和从左面看的图形如图1所示.
![]() 这个几何体可以是图2中甲,乙,丙中的______;
这个几何体可以是图2中甲,乙,丙中的______;
![]() 这个几何体最多由______个小正方体堆成,最少由______个小正方体堆成;
这个几何体最多由______个小正方体堆成,最少由______个小正方体堆成;
![]() 请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形.
请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com