
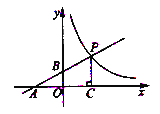
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别相交于
轴分别相交于![]() ,
,![]() 两点,与双曲线
两点,与双曲线![]() (
(![]() )相交于点
)相交于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() ,在点
,在点![]() 右侧的双曲线上取一点
右侧的双曲线上取一点![]() ,作
,作![]() 轴于
轴于![]() ,当以点
,当以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,则点
相似,则点![]() 的坐标是__________.
的坐标是__________.
【答案】![]() 或
或![]()
【解析】
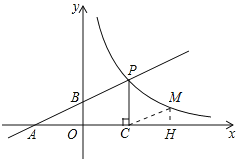
先求出点A、点B的坐标,设点M的坐标为(m,n),分两种情况:当△MCH∽△BAO和△MCH∽△ABO时,由相似得比例求出m的值,即可得出点M的坐标.
解:直线y=![]() x+1与x轴,y轴分别相交于A,B两点,
x+1与x轴,y轴分别相交于A,B两点,
令x=0得y=1,令y=0得x=-2,
∴A(-2,0),B(0,1).
设点M的坐标为(m,n),
∵点M在双曲线![]() 上,
上,
∴n=![]() .
.
当△MCH∽△BAO时,
可得![]() ,
,
即![]() ,
,
∴m-2=2n,即m-2=![]() ,
,
∴m2-2m-8=0,
解得:m1=4,m2=-2(舍去),
∴n=![]() =1,
=1,
∴M(4,1);
当△MCH∽△ABO时,
可得![]() ,
,
即![]()
整理得:2m-4=![]() ,
,
∴m2-2m-2=0,
解得:m1=1+![]() ,m2=1-
,m2=1-![]() (舍去),
(舍去),
∴n=![]() =
=![]() -2,
-2,
∴M(1+![]() ,
,![]() -2).
-2).
综上,M(4,1)或M(1+![]() ,
,![]() -2).
-2).
故答案为:(4,1)或(1+![]() ,
,![]() -2).
-2).


科目:初中数学 来源: 题型:
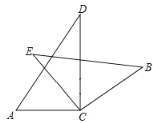
【题目】两块不同的三角板按如图所示摆放,两个直角顶点C重合,![]() ,
,![]() 。接着保持三角板ACD不动,将三角板CBE绕着点C旋转,但保证点E在直线AC的上方,若三角板CBE有一条边与斜边AD平行,则∠ACE=__________.
。接着保持三角板ACD不动,将三角板CBE绕着点C旋转,但保证点E在直线AC的上方,若三角板CBE有一条边与斜边AD平行,则∠ACE=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年是我市脱贫攻坚决战决胜的关键之年,阳高灵丘、云州三县区要在今年实现脱贫摘帽.近年来,享有“中国黄花之乡的云州区坚持把产业扶贫作为扶贫攻坚的重要支撑,黄花销售也成为区政府关注的一项民生工程.现有成本为每千克80元的大同特级黄花菜干货,经市场分析,若按每千克100元销售,一个月能售出800千克;销售单价每涨价1元,月销售量就减少10千克.针对黄花菜的销售情况,请解答以下问题.
(1)现计划在月销售成本不超过40000元的情况下,使得月销售利润达到24000元,销售单价应定为多少元?
(2)定价为多少元时,农民销售可获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形BCOG中,OC=3,点A为边OG上一点,OA=![]() ,AB,∠CBA=30°.动点D以每秒1个单位的速度从点C出发沿CO向终点O运动,同时动点E以每秒2个单位的速度从点A出发沿AB向终点B运动,过点D作DF∥AB,交BC于点F,连接AD、DE、EF,设运动时间为1秒.
,AB,∠CBA=30°.动点D以每秒1个单位的速度从点C出发沿CO向终点O运动,同时动点E以每秒2个单位的速度从点A出发沿AB向终点B运动,过点D作DF∥AB,交BC于点F,连接AD、DE、EF,设运动时间为1秒.
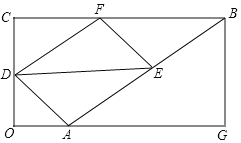
(1)求DF的长(用含t的代数式表示)
(2)求证:四边形ADFE为平行四边形;
(3)探索当t为何值时,△BEF与以D,E,F为顶点的三角形相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确结论的个数为( )
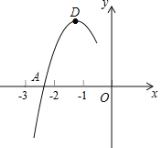
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)过以下三个点:(m,n),(m+2,2n),和(m+6,n),当抛物线上另有点的横坐标为m+4时,它的纵坐标为_____;当横坐标为m﹣2时,它的纵坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校园安全受到全社会的广泛关注,某市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
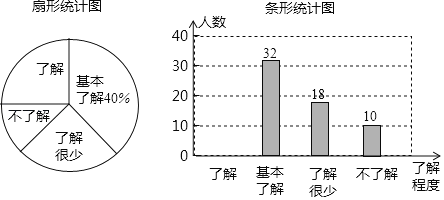
(1)在这次活动中抽查了多少名中学生?
(2)若该中学共有学生1600人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”程度的人数.
(3)若从对校园安全知识达到“了解程度的2个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com