
分析 (1)由题意将原方程组从新组合为$\left\{\begin{array}{l}{bx+ay=-8}\\{ax-by=-4}\end{array}\right.$和$\left\{\begin{array}{l}{2x+5y=-6}\\{3x-5y=16}\end{array}\right.$,然后解得$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$,并将其代入另一个方程组解得a,b的值即可;
(2)由一元二次方程有两个根可知△≥0,进而解得a的取值范围,然后根据a的范围化简原式得到答案.
解答 解:(1)∵关于x,y的方程组$\left\{\begin{array}{l}2x+5y=-6\\ ax-by=-4\end{array}$和$\left\{\begin{array}{l}3x-5y=16\\ bx+ay=-8\end{array}$的解相同,
∴方程组$\left\{\begin{array}{l}{bx+ay=-8}\\{ax-by=-4}\end{array}\right.$和$\left\{\begin{array}{l}{2x+5y=-6}\\{3x-5y=16}\end{array}\right.$的解相同,
∴解方程组$\left\{\begin{array}{l}{2x+5y=-6}\\{3x-5y=16}\end{array}\right.$得到$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$,
∴把$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{bx+ay=-8}\\{ax-by=-4}\end{array}\right.$得到$\left\{\begin{array}{l}{2b-2a=-8}\\{2a+2b=-4}\end{array}\right.$,
∴解方程组$\left\{\begin{array}{l}{2b-2a=-8}\\{2a+2b=-4}\end{array}\right.$得到$\left\{\begin{array}{l}{a=1}\\{b=-3}\end{array}\right.$,
∴(2a+b)2015=(-1)2015=-1;
(2)∵关于x的方程x2-2ax+a2+a-1=0有两个实数根,
∴△≥0,
∴(-2a)2-4(a2+a-1)≥0,
∴-4a+4≥0,即a≤1,
∴a-1≤0,a-2≤-1,
∴原式=$\sqrt{(a-1)^{2}}$-|a-2|=-(a-1)+a-2=-1.
点评 本题考查了:1、熟练掌握二元一次方程组的定义极其解法;2、利用一元二次方程根的判别式(△=b2-4ac)判断方程的根的情况.一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.3、二次根式的性质与化简.本题难度不大,计算过程中需细心.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
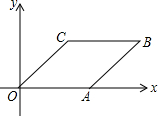 菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,点A的坐标为($\sqrt{2}$,0),则点B的坐标为( )
菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,点A的坐标为($\sqrt{2}$,0),则点B的坐标为( )| A. | ($\sqrt{2}$,1) | B. | (1,$\sqrt{2}$) | C. | (1,$\sqrt{2}$+1) | D. | ($\sqrt{2}$+1,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com