
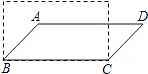
 如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最大内角等于150°.
如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最大内角等于150°. 分析 首先过点A作AE⊥BC于点E,由将四根木条钉成的矩形木框变成平行四边形ABCD的形状,并使其面积为矩形面积的一半,可得AE=$\frac{1}{2}$AB,即可求得∠ABC的度数,继而求得各内角度数.
解答 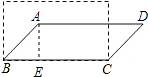 解:过点A作AE⊥BC于点E,
解:过点A作AE⊥BC于点E,
∵将四根木条钉成的矩形木框变成平行四边形ABCD的形状,并使其面积为矩形面积的一半,
∴AE=$\frac{1}{2}$AB,
∴∠ABC=30°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠BAD=180°-∠ABC=150°,
∴这个平行四边形的最大内角等于150°.
故答案为:150°.
点评 此题考查了平行四边形的性质以及矩形的性质.注意根据题意求得AE=$\frac{1}{2}$AB是关键.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{m}{m-3}$ | B. | $\frac{m}{3-m}$ | C. | $-\frac{m}{m+3}$ | D. | $\frac{m}{m+3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
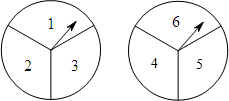 为了纪念中国共产主义青年团成立90周年,某校初三(1)、(2)班团支部组织了一次联欢会,小乐为活动设计了一个游戏:把两个可以自由转动的转盘各等分成三个扇形,分别标上1,2,3和4,5,6,每班级各派一名选手参加,每人同时转动两个转盘各一次(指针落在等分线上重转),转盘停止后,指针指向的数字之和为偶数时(1)班获胜,数字之和为奇数时(2)班获胜,小乐设计的游戏规则公平吗?请用树状图或列表分析说明,若认为不公平,请修改规则使游戏变得公平.
为了纪念中国共产主义青年团成立90周年,某校初三(1)、(2)班团支部组织了一次联欢会,小乐为活动设计了一个游戏:把两个可以自由转动的转盘各等分成三个扇形,分别标上1,2,3和4,5,6,每班级各派一名选手参加,每人同时转动两个转盘各一次(指针落在等分线上重转),转盘停止后,指针指向的数字之和为偶数时(1)班获胜,数字之和为奇数时(2)班获胜,小乐设计的游戏规则公平吗?请用树状图或列表分析说明,若认为不公平,请修改规则使游戏变得公平.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
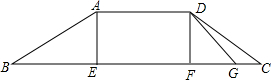 为了方便行人,市政府打算修建如图所示的过街天桥,桥面AD平行于地面BC,立柱AE⊥BC于点E,立柱DF⊥BC于点F,若AB=5$\sqrt{5}$米,tanB=$\frac{1}{2}$,∠C=30°.
为了方便行人,市政府打算修建如图所示的过街天桥,桥面AD平行于地面BC,立柱AE⊥BC于点E,立柱DF⊥BC于点F,若AB=5$\sqrt{5}$米,tanB=$\frac{1}{2}$,∠C=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com