
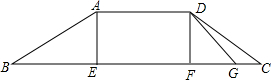
 Ϊ�˷������ˣ���������������ͼ��ʾ�Ĺ������ţ�����ADƽ���ڵ���BC������AE��BC�ڵ�E������DF��BC�ڵ�F����AB=5$\sqrt{5}$�ף�tanB=$\frac{1}{2}$����C=30�㣮
Ϊ�˷������ˣ���������������ͼ��ʾ�Ĺ������ţ�����ADƽ���ڵ���BC������AE��BC�ڵ�E������DF��BC�ڵ�F����AB=5$\sqrt{5}$�ף�tanB=$\frac{1}{2}$����C=30�㣮���� ��1����Rt��ABE�У�����tanB=$\frac{AE}{BE}$�õ�AB=$\sqrt{{AE}^{2}+{BE}^{2}}$���Ӷ���$\sqrt{5}$x=5$\sqrt{5}$���ݴ˼������AE�ij���
��2���жϳ��ı���AEFD�Ǿ��Σ���Rt��DCF�У��������Ǻ������
��� �⣺��1����ͼ����Rt��ABE�У�tanB=$\frac{AE}{BE}$=$\frac{1}{2}$��
����AE=x��BE=2x��
��AB=$\sqrt{{AE}^{2}+{BE}^{2}}$��
$\sqrt{5}$x=5$\sqrt{5}$��
���x=5��
��AE=5�ף�������AD�����BC֮��ľ���Ϊ5�ף�
��2����ͼ����AE��BC��DF��BC��
��AE��DF����AEF=90�㣬
��AD��BC��
���ı���AEFD�Ǿ��Σ�
��DF=AE=5�ף�
��Rt��DCF�У���C=30�㣬DF=5�ף�
��GF=$\frac{DF}{tan40��}$��5.95�ף�
��DF=AE=5����DCF=30�㣬
��CF=$\frac{DF}{tan30��}$=$\frac{5}{\frac{\sqrt{3}}{3}}$��8.66�ף�
��Ľ���ʡ��ռ·��Ŀ���ΪCG=CF-GF=8.66-5.95��2.7�ף�
���� ���⿼���˽�ֱ�������ε�Ӧ��--�¶��½����⣬�ҵ����ʵ�ֱ���������ǽ���Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
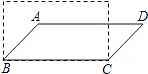 ��ͼ�������ĸ�ľ�����ɵľ���ľ����ƽ���ı���ABCD����״����ʹ�����Ϊ���������һ�룬�����ƽ���ı��ε�����ڽǵ���150�㣮
��ͼ�������ĸ�ľ�����ɵľ���ľ����ƽ���ı���ABCD����״����ʹ�����Ϊ���������һ�룬�����ƽ���ı��ε�����ڽǵ���150�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
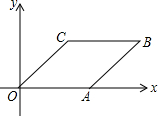 ����OABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ����AOC=45�㣬��A������Ϊ��$\sqrt{2}$��0�������B������Ϊ��������
����OABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ����AOC=45�㣬��A������Ϊ��$\sqrt{2}$��0�������B������Ϊ��������| A�� | ��$\sqrt{2}$��1�� | B�� | ��1��$\sqrt{2}$�� | C�� | ��1��$\sqrt{2}$+1�� | D�� | ��$\sqrt{2}$+1��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com