
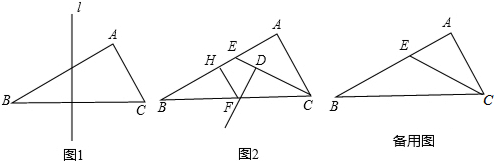
分析 (1)根据轴对称的性质画出即可;
(2)过点F作FG⊥CA于点G,求出四边形HFGA为矩形.推出FH=AG,FG∥AB求出∠GFC=∠EBC,根据线段垂直平分线的性质得出BE=EC,求出∠ECB=∠EBC=∠GFC,∠FDC=∠A=90°,∠FDC=∠FGC=90°,根据AAS推出△FGC≌△CDF,推出CG=FD即可;
(3)过F作FH⊥BA于H,过点C作CG⊥FH于G,求出四边形ACGH为矩形.推出AC=GH,CG∥AB,证△FGC≌△CDF,根据全等三角形的性质得出FG=FD,即可得出答案.
解答 解:(1)如图: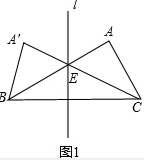 ;
;
(2)①DF+FH=CA,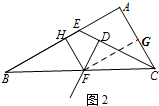
证明:过点F作FG⊥CA于点G,
∵FH⊥BA于H,∠A=90°,FG⊥CA,
∴∠A=∠FGA=∠FHA=90°,
∴四边形HFGA为矩形.
∴FH=AG,FG∥AB,
∴∠GFC=∠EBC,
∵直线l是BC的垂直平分线,
∴BE=EC,
∴∠EBC=∠ECB,
由(1)和平移可知,
∠ECB=∠EBC=∠GFC,
∠FDC=∠A=90°,
∴∠FDC=∠FGC=90°.
∵在△FGC和△CDF中
$\left\{\begin{array}{l}{∠GFC=∠DCF}\\{∠FGC=∠CDF}\\{CF=CF}\end{array}\right.$
∴△FGC≌△CDF,
∴CG=FD,
∴DF+FH=GC+AG,
即DF+FH=AC;
②解:FH-DF=AC,
理由是:过F作FH⊥BA于H,过点C作CG⊥FH于G,
∵FH⊥BA于H,∠BAC=90°,CG⊥FH,
∴∠CAH=∠CGH=∠FHA=90°,
∴四边形ACGH为矩形.
∴AC=GH,CG∥AB,
∴∠GCF=∠EBC,
∵直线l是BC的垂直平分线,
∴BE=EC,
∴∠EBC=∠ECB=∠FCD,
∴∠GCF=∠FCD,
由(1)和平移可知,∠FDC=∠A=90°,
∴∠FDC=∠FGC=90°.
∵在△FGC和△CDF中
$\left\{\begin{array}{l}{∠GFC=∠DCF}\\{∠FGC=∠CDF}\\{CF=CF}\end{array}\right.$
∴△FGC≌△CDF,
∴FG=FD,
∵FH-FG=GH,
∴FH-DF=AC.
点评 本题考查了平移的性质,线段垂直平分线性质,全等三角形的性质和判定,等腰三角形的性质的应用,能综合运用性质进行推理是解此题的关键,此题是一道综合性比较强的题目,难度偏大.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
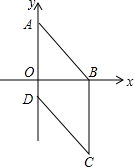 如图,在平面直角坐标系中,四边形ABCD是菱形,已知A(0,4),B(3,0).
如图,在平面直角坐标系中,四边形ABCD是菱形,已知A(0,4),B(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (80-x)(200+8x)=8450 | B. | (40-x)(200+8x)=8450 | ||
| C. | (40-x)(200+40x)=8450 | D. | (40-x)(200+x)=8450 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
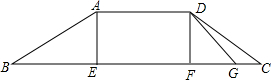 为了方便行人,市政府打算修建如图所示的过街天桥,桥面AD平行于地面BC,立柱AE⊥BC于点E,立柱DF⊥BC于点F,若AB=5$\sqrt{5}$米,tanB=$\frac{1}{2}$,∠C=30°.
为了方便行人,市政府打算修建如图所示的过街天桥,桥面AD平行于地面BC,立柱AE⊥BC于点E,立柱DF⊥BC于点F,若AB=5$\sqrt{5}$米,tanB=$\frac{1}{2}$,∠C=30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 平均数$\overline{x}$ | 8.5 | 9 | 9 | 8.5 |
| 方差S2 | 1 | 1.2 | 1 | 1.3 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com