
科目:初中数学 来源: 题型:解答题
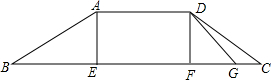 为了方便行人,市政府打算修建如图所示的过街天桥,桥面AD平行于地面BC,立柱AE⊥BC于点E,立柱DF⊥BC于点F,若AB=5$\sqrt{5}$米,tanB=$\frac{1}{2}$,∠C=30°.
为了方便行人,市政府打算修建如图所示的过街天桥,桥面AD平行于地面BC,立柱AE⊥BC于点E,立柱DF⊥BC于点F,若AB=5$\sqrt{5}$米,tanB=$\frac{1}{2}$,∠C=30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 平均数$\overline{x}$ | 8.5 | 9 | 9 | 8.5 |
| 方差S2 | 1 | 1.2 | 1 | 1.3 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
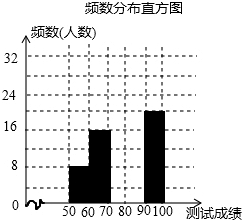 苏州某中学为了迎接第53届世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:
苏州某中学为了迎接第53届世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 8 |
| 第2组 | 60≤x<70 | 16 |
| 第3组 | 70≤x<80 | a |
| 第4组 | 80≤x<90 | 32 |
| 第5组 | 90≤x<100 | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com