练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
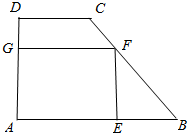
    14．如图，有一块梯形铁板ABCD，AB∥CD，∠A=90°，AB=6cm，CD=2cm，AD=4cm，现在梯形中剪出一内接矩形铁板AEFG，其中E在AB上，F在BC上，G在AD上．若矩形面积为9cm2，则矩形的一边EF长为多少？

    分析 作CH⊥AB于H，由条件可以得出四边形ADCH为矩形，根据矩形的性质就可以求出CH、BH的长，设EF=x，则BE=x，AE=6-x，根据矩形的面积公式就可以建立等式，从而求出其解．

    解答 解：过C作CH⊥AB于H．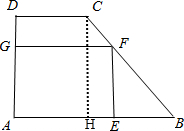

    在直角梯形ABCD中，DC∥AB，∠ADC=90°，
    ∴四边形ADCH为矩形．
    ∴CH=AD=2cm，BH=AB-CD=6-2=4cm．
    ∴CH=BH．
    设EF=x，则BE=x，AE=6-x，由题意，得
    x（6-x）=9
    整理得：x2-6x+9=0，
    解得：x1=x2=3
    ∴矩形的一边EF长为3cm．

    点评 此题考查了直角梯形的性质，矩形的性质，矩形的面积公式的运用，在解答时根据面积建立方程求解这是在几何图形中列一元二次方程求解的常用方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    4．已知∠A=20°，则∠A的余角等于70°度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．已知点P（-2，3）和点Q（a，b）关于原点对称，则a+b=（　　）
    A．1B．-1C．5D．-5

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如图，在△ABC中，AB所对的角是∠ACB；在△ABF中，AB边所对的角是∠AFB；∠ACB所对的边有AF和AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知y=a（x-t-1）2+t2（a，t是常数，a≠0，t≠0）的图象的顶点是A，y=（x-1）2的顶点是B．
    （1）判断点A是否在y=（x-1）2的图象上，为什么？
    （2）若y=a（x-t-1）2+t2（a≠0，t≠0）的图象经过点B，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，C为线段AB的中点，点P从点A出发以acm/s的速度沿AB向点B运动，同时，点Q从点B出发以bcm/s（b＜a）的速度沿BA向点A运动，点Q运动的时间为t s，点P与点Q在点D相遇，AB=6CD．
    （1）求$\frac{b}{a}$的值；
    （2）点E为BQ的中点，当t=4（点P，Q在运动的过程中）时，PB=44cm，CE=26cm，求AB长及a值；
    （3）在（2）的条件下，当点P与点E相遇时，点P停止运动，在点P与点E相遇的时刻，点R从点D出发以3cm/s的速度沿DA向A运动，点P停止运动后，当t为何值时，RQ=$\frac{1}{2}$PE？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

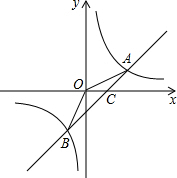    4．已知反比例函数y=$\frac{k}{2x}$和一次函数y=kx-1交于A、B两点，其中A点坐标为（1，b）．
    （1）求反比例函数和一次函数的解析式；
    （2）已知点B的横坐标为-$\frac{1}{2}$，求△AOB的面积；
    （3）在x轴上是否存在点P，使△AOP为等腰三角形？若存在，把符合条件的P点坐标都求出来；如不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图1，△ABC中，沿∠BAC的平分线AB1折叠，点B落在A1处．剪掉重叠部分；将余下部分沿∠B1A1C的平分线A1B2折叠，点B1落在A2处．剪掉重叠部分；…；将余下部分沿∠BnAnC的平分线AnBn+1折叠，点Bn与点C重合，无论折叠多少次，只要最后一次恰好重合，∠BAC是△ABC的好角．
    小丽展示了确定∠BAC是△ABC的好角的两种情形．情形一：如图2，沿等腰三角形ABC顶角∠BAC的平分线AB1折叠，点B与点C重合；情形二：如图3，沿∠BAC的平分线AB1折叠，剪掉重叠部分；将余下部分沿∠B1A1C的平分线A1B2折叠，此时点B1与点C重合．
    （1）情形二中，∠B与∠C的等量关系∠B=2∠C．
    （2）若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C的等量关系∠B=n∠C．
    （3）如果一个三角形的最小角是4°，直接写出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．
    答：4、172；8、168；16、160；44、132；88°、88°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．方程组$\left\{\begin{array}{l}{x-y=-1}\\{ax-by=5}\end{array}\right.$和方程组$\left\{\begin{array}{l}{x+2y=8}\\{ax+by=11}\end{array}\right.$的解相同，求ab．

    查看答案和解析>>

    同步练习册答案