
【题目】已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
(1)求证:BC与⊙O相切;
(2)求阴影部分面积. 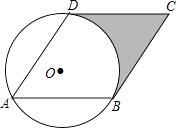
【答案】
(1)证明:连结OB、OD、OC,
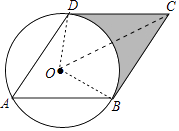
∵ABCD是菱形,
∴CD=CB,
∵OC=OC,OD=OB,
∴△OCD≌△OCB,
∴∠ODC=∠OBC,
∵CD与⊙O相切,∴OD⊥CD,
∴∠OBC=∠ODC=90°,
即OB⊥BC,点B在⊙O上,
∴BC与⊙O相切.
(2)解:∵ABCD是菱形,
∴∠A=∠DCB,
∵∠DOB与∠A所对的弧都是 ![]() ,
,
∴∠DOB=2∠A,
由(1)知∠DOB+∠C=180°,
∴∠DOB=120°,∠DOC=60°,
∵OD=1,∴OC=2,DC= ![]()
∴S阴影=2S△DOC﹣S扇形OBD=2× ![]() ×1×
×1× ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() π.
π.
【解析】(1)连结OB、OD、OC,只要证明△OCD≌△OCB,推出∠ODC=∠OBC,由CD与⊙O相切推出OD⊥CD,推出∠OBC=∠ODC=90°,由此即可证明;(2)根据S阴影=2S△DOC﹣S扇形OBD计算即可;
【考点精析】通过灵活运用菱形的性质和扇形面积计算公式,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图, ![]() 是
是 ![]() 的中线,
的中线, ![]() 是线段
是线段 ![]() 上一点(不与点
上一点(不与点 ![]() 重合).
重合). ![]() 交
交 ![]() 于点
于点 ![]() ,
, ![]() ,连结
,连结 ![]() .
.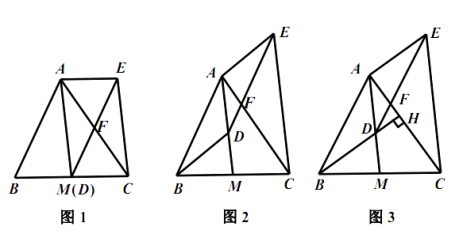
(1)如图1,当点 ![]() 与
与 ![]() 重合时,求证:四边形
重合时,求证:四边形 ![]() 是平行四边形;
是平行四边形;
(2)如图2,当点 ![]() 不与
不与 ![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长 ![]() 交
交 ![]() 于点
于点 ![]() ,若
,若 ![]() ,且
,且 ![]() .当
.当 ![]() ,
, ![]() 时,求
时,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商人制成了一个如图所示的转盘,取名为“开心大转盘”,游戏规定:参与者自由转动转盘,转盘停止后,若指针指向字母“A”,则收费2元,若指针指向字母“B”,则奖励3元;若指针指向字母“C”,则奖励1元.一天,前来寻开心的人转动转盘80次,你认为该商人是盈利的可能性大还是亏损的可能性大?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明袋子中有1个红球、1 个绿球和n个白球,这些球除颜色外都相同.
(1)从袋中随机摸出1个球,记录下颜色后放回袋子中并搅匀,不断重复该试验.发现摸到白球的频率稳定在0.75,则n的值为;
(2)当n=2时,把袋中的球搅匀后任意摸出2个球,求摸出的2个球颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( )
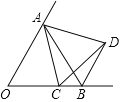
A. 平行 B. 相交 C. 垂直 D. 平行、相交或垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.

(1)求该一次函数的解析式;
(2)求点C和点D的坐标;
(3)求△AOB的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
(1)写出数轴上点B所表示的数 ;
(2)点P所表示的数 ;(用含t的代数式表示);
(3)M是AP的中点,N为PB的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,说明理由;若不变,请你画出图形,并求出线段MN的长.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com