练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列计算结果正确的是（　　）

    A.﹣2x2y3x3y3＝﹣2x6y9B.12x6y4÷2x3y3＝6x3y

    C.3x3y2﹣x2y3＝xyD.（﹣2a﹣3）（2a﹣3）＝4a2﹣9

    【答案】B

    【解析】

    根据单项式乘单项式法则、单项式除以单项式法则、同类项的定义和平方差公式逐一判断即可．

    ∵﹣2x2y3x3y3＝﹣2x5y6，故选项A错误；

    ∵12x6y4÷2x3y3＝6x3y，故选项B正确；

    ∵3x3y2和x2y3不是同类项，不能合并，故选项C错误；

    ∵（﹣2a﹣3）（2a﹣3）＝﹣4a2+9，故选项D错误；

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点F是CD 的中点，且AF⊥CD，BC=ED，∠BCD=∠EDC．

    （1）求证：BF=EF；

    （2）求证：AB=AE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小红和小明在研究一个数学问题：已知AB∥CD，AB和CD都不经过点E，探索∠E与∠A，∠C的数量关系．
    （1）发现：在图1中，小红和小明都发现：∠AEC=∠A+∠C； 小红是这样证明的：如图7过点E作EQ∥AB．
    ∴∠AEQ=∠A（）
    ∵EQ∥AB，AB∥CD．
    ∴EQ∥CD（）
    ∴∠CEQ=∠C
    ∴∠AEQ+∠CEQ=∠A+∠C 即∠AEC=∠A+∠C．
    小明是这样证明的：如图7过点E作EQ∥AB∥CD．
    ∴∠AEQ=∠A，∠CEQ=∠C
    ∴∠AEQ+∠CEQ=∠A+∠C即∠AEC=∠A+∠C
    请在上面证明过程的横线上，填写依据：
    两人的证明过程中，完全正确的是 ．
    （2）尝试： ①在图2中，若∠A=110°，∠C=130°，则∠E的度数为；
    ②在图3中，若∠A=20°，∠C=50°，则∠E的度数为 ．
    （3）探索： 装置图4中，探索∠E与∠A，∠C的数量关系，并说明理由．
    （4）猜想： 如图5，∠B、∠D、∠E、∠F、∠G之间有什么关系？（直接写出结论）
    （5）如图6，你可以得到什么结论？（直接写出结论）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】任何一个凸多边形的外角和等于____．它与该多边形的__无关．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店需要购进甲、乙两种商品共180件，其进价和售价如表：（注：获利=售价﹣进价）

    甲

    乙

    进价（元/件）

    14

    35

    售价（元/件）

    20

    43


    （1）若商店计划销售完这批商品后能获利1240元，问甲、乙两种商品应分别购进多少件？
    （2）若商店计划投入资金少于5040元，且销售完这批商品后获利多于1312元，请问有哪几种购货方案？并直接写出其中获利最大的购货方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，线段AB是⊙O的直径，BC⊥CD于点C，AD⊥CD于点D，请仅用无刻度的直尺按下列要求作图．

    （1）在图1中，当线段CD与⊙O相切时，请在CD上确定一点E，连接BE，使BE平分∠ABC；

    （2）在图2中，当线段CD与⊙O相离时，请过点O作OF⊥CD，垂足为F．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：已知等边△ABC中，D是AC的中点，E是BC延长线上的一点，且CE=CD，DM⊥BC，垂足为M．

    （1）求∠E的度数．

    （2）求证：M是BE的中点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

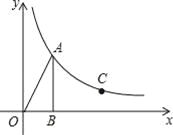
    【题目】如图，在平面直角坐标系中，Rt△OAB的顶点B在x轴的正半轴上，已知∠OBA=90°，OB=3，sin∠AOB=．反比例函数y=（x＞0）的图象经过点A．

    （1）求反比例函数的解析式；

    （2）若点C（m，2）是反比例函数y=（x＞0）图象上的点，则在x轴上是否存在点P，使得PA+PC最小？若存在，求出点P的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

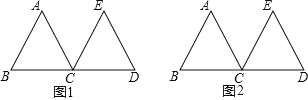
    【题目】如图，等边△ABC和等边△ECD的边长相等，BC与CD两边在同一直线上，请根据如下要求，使用无刻度的直尺，通过连线的方式画图．

    （1）在图1中画出一个直角三角形．（2）在图2中过点C作BD的垂线．

    查看答案和解析>>

    同步练习册答案