【题目】今年是“精准扶贫”攻坚关键年，某扶贫工作队为对口扶贫村引进建立了一村集体企业，并无偿提供一笔无息贷款作为启动资金，双方约定：①企业生产出的产品全部由扶贫工作队及时联系商家收购；②企业从生产销售的利润中，要保证按时发放工人每月最低工资32000元．已知该企业生产的产品成本为20元/件，月生产量y（千件）与出厂价x（元）（25≤x≤50）的函数关系可用图中的线段AB和BC表示，其中AB的解析式为y=﹣x+m（m为常数）．

（1）求该企业月生产量y（千件）与出厂价x（元）之间的函数关系式，并写出自变量x的取值范围．

（2）当该企业生产出的产品出厂价定为多少元时，月利润W（元）最大？最大利润是多少？[月利润=（出厂价﹣成本）×月生产量﹣工人月最低工资]．

参考答案：

【答案】（1）y=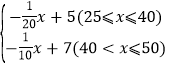；（2）45, 最大利润是45元.

【解析】试题分析：（1）把（40，3）代入y=-x+m得，3=-×40+m，求得y=-x+5，（25≤x≤40），设BC的解析式为：y=kx+b，把（40，3），（50，2）代入y=kx+b得得到y=-x+7，（40＜x≤50）；

（2）设该企业生产出的产品出厂价定为x元时，月利润W（元）最大，根据题意得到二次函数的解析式，求得当x=40时，W最大=30299元，当x=45时，W最大=32342.5元，即可得到结论．

(1)把(40,3)代入y=x+m得,3=×40+m，

∴m=5，

∴y=x+5,(25x40)，

设BC的解析式为：y=kx+b，

把(40,3),(50,2)代入y=kx+b得,，

解得，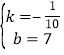

∴y=110x+7,(40<x50)，

综上所述：y=；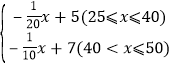

(2)设该企业生产出的产品出厂价定为x元时,月利润W(元)最大，

根据题意得,W=(x+5)(x20)32000=x2+6x32100=120(x60)2+33900，

∵25x40，

∴当x=40时,W最大=30299元，

W=(x+7)(x20)32000=x2+9x32140= (x45)+32342.5，

∵40<x50，

∴当x=45时,W最大=32342.5元，

∵30299<32342.5，

∴当该企业生产出的产品出厂价定为45元时,月利润W(元)最大，最大利润是34342.5元。

关闭