
【题目】△ABC,△DEC均为直角三角形,B,C,E三点在一条直线上,过D作DM⊥AC于M.

(1)如图1,若△ABC≌△DEC,且AB=2BC.
①过B作BN⊥AC于N,则线段AN,BN,MN之间的数量关系为: ;(直接写出答案)
②连接ME,求![]() 的值;
的值;
(2)如图2,若AB=CE=DE,DM=2,MC=1,求ME的长.
【答案】(1)①AN﹣BN=MN;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①由题意先证得四边形ABED是正方形,再通过“角角边”证明△ABN≌△DAM,即AM=BN,则AN﹣BN=AN﹣AM= MN;
②连接ME,求![]() 的值;
的值;
(2)如图2,过E作EG⊥DM于G,EH⊥AC于H,过C作CF⊥ME于F,通过“角角边”证得△CEH≌△DEG,即GE=HE,则四边形MHEG是正方形,所以∠CMF=45°,在Rt△CFM中求得CF=MF=![]() ,在Rt△CDM中求得CD=
,在Rt△CDM中求得CD=![]() ,Rt△CEF中求得EF=
,Rt△CEF中求得EF=![]() ,然后用MF+EF即可得解.
,然后用MF+EF即可得解.
(1)①如图1,连接AD,

∵△ABC≌△DEC,
∴AB=2BC=2CE=BE,
又∵∠ABC=∠DEC=90°,
∴AB∥DE,
∴四边形ABED是正方形,
∴AD=BE=AB,∠BAD=90°,
又∵BN⊥AC,DM⊥AC,
∴∠DMA=∠ANB=90°,∠BAN+∠DAM=∠ADM+∠DAM=90°,
∴∠BAN=∠ADM,
∴△ABN≌△DAM(AAS),
∴AM=BN,
∵AN﹣AM=MN,
∴AN﹣BN=MN,
故答案为:AN﹣BN=MN;
②如图,延长AC,交DE的延长线于F,

由∠ABC=∠FEC=90°,BC=EC,∠ACB=∠FCE,可得△ABC≌△FEC,
∴EF=AB=DE,
∴E是DF的中点,
又∵∠DMF=90°,
∴Rt△DMF中,ME=![]() DF=DE,
DF=DE,
又∵CE=![]() BE=
BE=![]() DE,
DE,
∴![]() =
=![]() ;
;
(2)如图2,过E作EG⊥DM于G,EH⊥AC于H,过C作CF⊥ME于F,

则∠DGE=∠H=90°,
∴∠HEG=90°=∠CED,
∴∠CEH=∠DEG,
又∵CE=DE,
∴△CEH≌△DEG(AAS),
∴GE=HE,
∴四边形MHEG是正方形,
∴∠CMF=45°,
∵MC=1,
∴CF=MF=![]() ,
,
在Rt△CDM中,CD=![]() ,
,
∴CE=DE=![]() ,
,
又∵Rt△CEF中,EF=![]() =
=![]() ,
,
∴ME=MF+EF=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,那么∠DAC的度数为( )

A. 90° B. 80° C. 70° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明准备进行如下操作实验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为S,作△ABC边中线AC1,取AB的中点A1,连接A1C1得到第一个三角形△A1BC1,作△A1BC1中线A1C2,取A1B的中点A2,连接A1C2得到第二个三角形△A2BC2………,重复这样的操作,则第2019个三角形△A2019BC2019的面积是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知△ABC,以AB、AC为边向△ABC外作等边三角形ABD和等边三角形ACE,连接BE、CD.请你完成图形,并证明:BE=CD;

(2)如图(2),已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE、CD,BE和CD有什么数量关系?说明理由;
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:如图(3),要测量河两岸相对的两点B、E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=1千米,AC=AE.求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(2,3),则经过第2018次变换后所得的A点坐标是________.
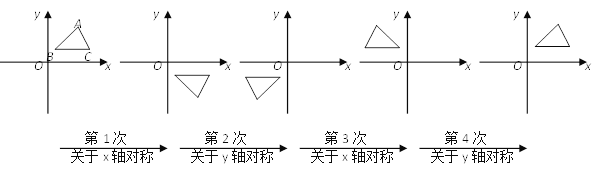
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D,E是△ABC内的两点,AD平分∠BAC,∠EBC=∠E=60°.若BE=9cm,DE=3cm,则BC的长为 ( )

A.12cmB.11cmC.9cmD.6cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com