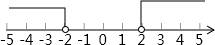解下列不等式:
(1)|x|≤5,
(2)|x|>2.
解:(1)当x>0时,x≤5,
此时不等式的解集为0<x≤5;
当x=0时,0≤5,此时x=0
当x<0时,x≥-5,
此时不等式的解集为-5≤x<0.
综上所述,不等式解集为:-5≤x≤5.
(2)当x>0时,x>2,此时不等式的解集为x>2,
当x=0时,0>2,此时不等式无解,
当x<0时,x<-2,此时不等式的解集为x<-2,
综上所述,不等式解集为:x>2或x<-2,
另解:我们还可以利用绝对值的几何意义得出上两题的解集.
(1)如图所示:

不等式解集为:-5≤x≤5;
(2)不等式解集为x>2或x<-2.
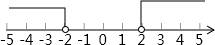
一般地,如果a>0,不等式|x|>a的解集为x>a或x<-a,|x|<a的解集为-a<x<a;
如果a<0,不等式|x|>a的解为有任意解,|x|<a的解集为无解.
分析:本题首先根据绝对值的性质去掉绝对值符号,再根据不等式的基本性质求出其解集即可.
点评:本题考查的是解带绝对值的一元一次不等式,解答此类题目时首先要根据绝对值的性质去掉绝对值符号,再根据不等式的基本性质求不等式的解集.