练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，圆内接四边形ABCD的BA，CD的延长线交于P，AC，BD交于E，则图中相似三角形有(　　)

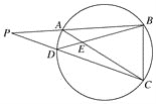
    A. 2对 B. 3对 C. 4对 D. 5对

    【答案】C

    【解析】

    根据有两个角对应相等的三角形是相似三角形即可解题.

    根据同弧所对的圆周角相等可得，∠EAB=∠EDC，∠ABE=∠ECD，所以△ABE∽△DCE；

    ∠ADE=∠BCE，∠DAE=∠CBE，所以△ADE∽△BCE；

    ∠APC=∠DPB，∠ACP=∠DBP，所以△PAC∽△PDB；

    根据圆内接四边形对角互补可得∠ADC+∠CBP=180°，因为∠ADC+∠ADP=180°，所以∠ADP=∠CBP，又因为∠APD=∠CPB，所以△ADP∽△CBP .综上所述，相似三角形共有4对.

    故本题正确答案为C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】截长补短法，是初中几何题中一种添加辅助线的方法，也是把几何题化难为易的一种策略．截长就是在长边上截取一条线段与某一短边相等，补短就是通过延长或旋转等方式使两条短边拼合到一起，从而解决问题．

    （1）如图1，△ABC是等边三角形，点D是边BC下方一点，∠BDC＝120°，探索线段DA、DB、DC之间的数量关系．

    解题思路：延长DC到点E，使CE＝BD，根据∠BAC+∠BDC＝180°，可证∠ABD＝∠ACE，易证△ABD≌△ACE，得出△ADE是等边三角形，所以AD＝DE，从而解决问题．

    根据上述解题思路，三条线段DA、DB、DC之间的等量关系是；（直接写出结果）

    （2）如图2，Rt△ABC中，∠BAC＝90°，AB＝AC．点D是边BC下方一点，∠BDC＝90°，探索三条线段DA、DB、DC之间的等量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

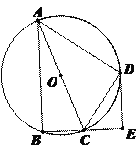
    【题目】如图，四边形ABCD是⊙O的内接四边形， ，AC为直径， DE⊥BC，垂足为E．

    （1）求证：CD平分∠ACE；

    （2）若AC＝9，CE＝3，求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，正方形OABC的边长为4，顶点A，C分别在x轴、y轴的正半轴上，抛物线y＝－x2＋bx＋c经过点B，C两点，点D为抛物线的顶点，连接AC，BD，CD.

    (1)求此抛物线的解析式；

    (2)求此抛物线顶点D的坐标和四边形ABDC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是由8个大小相同的小正方体组合成的简单几何体．

    （1）该几何体的主视图如图所示，请在下面方格纸中分别画出它的左视图和俯视图；（边框线加粗画出，并涂上阴影）

    （2）如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的俯视图和主视图不变，那么请在下列网格图中画出添加小正方体后所得几何体所有可能的左视图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

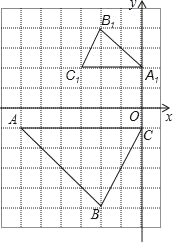
    【题目】如图，△ABC与△A1B1C1是位似图形．

    （1）在网格上建立平面直角坐标系，使得点A的坐标为（﹣6，﹣1），点C1的坐标为（﹣3，2），则点B的坐标为　 　；

    （2）以点A为位似中心，在网格图中作△AB2C2，使△AB2C2和△ABC位似，且位似比为1：2；

    （3）在图上标出△ABC与△A1B1C1的位似中心P，并写出点P的坐标为　 　，计算四边形ABCP的周长为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线l1：y＝﹣x与反比例函数y＝的图象交于A，B两点（点A在点B左侧），已知A点的纵坐标是2；

    （1）求反比例函数的表达式；

    （2）根据图象直接写出﹣x＞的解集；

    （3）将直线l1：y＝- x沿y向上平移后的直线l2与反比例函数y＝在第二象限内交于点C，如果△ABC的面积为30，求平移后的直线l2的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

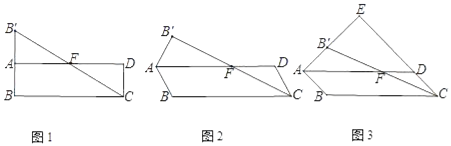
    【题目】在ABCD中，点B关于AD的对称点为B′，连接AB′，CB′，CB′交AD于F点．

    （1）如图1，∠ABC=90°，求证：F为CB′的中点；

    （2）小宇通过观察、实验、提出猜想：如图2，在点B绕点A旋转的过程中，点F始终为CB′的中点．小宇把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：

    想法1：过点B′作B′G∥CD交AD于G点，只需证三角形全等；

    想法2：连接BB′交AD于H点，只需证H为BB′的中点；

    想法3：连接BB′，BF，只需证∠B′BC=90°．

    …

    请你参考上面的想法，证明F为CB′的中点．（一种方法即可）

    （3）如图3，当∠ABC=135°时，AB′，CD的延长线相交于点E，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

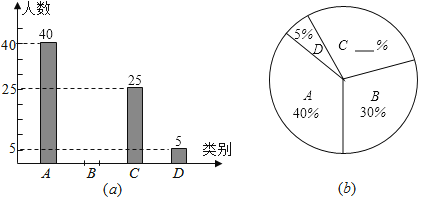
    【题目】为了了解某区2018年初中毕业生毕业后的去向，某区教育部门对部分初三学生进行了抽样调查，就初三学生的四种去向（A，读普通高中；B，读职业高中；C，直接进入社会就业；D，其它）进行数据统计，并绘制了两幅不完整的统计图（a）、（b）．请问：

    （1）此次共调查了多少名初中毕业生？

    （2）将两幅统计图中不完整的部分补充完整；

    （3）若某区2018年初三毕业生共有3500人，请估计2019年初三毕业生中读普通高中的学生人数．

    查看答案和解析>>

    同步练习册答案