
分析 分成a≥0和a<0两种情况进行讨论,化简后即可求解.
解答 解:当a≥0时,原式即$\frac{x}{3}$+a=$\frac{a}{2}$x-$\frac{1}{6}$x+1,
即($\frac{1}{2}$-$\frac{a}{2}$)x=1-a.
当$\frac{1}{2}$-$\frac{a}{2}$=0时a=1,此时1-a=0,方程有无数解;
当a<0时,原式即$\frac{x}{3}$+a=-$\frac{a}{2}$x-$\frac{1}{6}$x+1,
即($\frac{1}{2}$+$\frac{a}{2}$)x=1-a,
当$\frac{1}{2}$+$\frac{a}{2}$=0时a=-1,此时1-a=-2≠0,方程无解.
总之,当a=-1方程无解;
当a=1时方程有无数解.
点评 本题考查了一元一次方程的解,对a进行讨论是关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
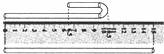 如图,直尺的下面是吸管的展直状态(最大长度),上面是该吸管的包装状态(外侧绷紧),弯曲部分可视为一半圆环,设其外圆半径为xcm,则根据题意可列方程为6.5+2(10.5-6.5-x)+πx=15.
如图,直尺的下面是吸管的展直状态(最大长度),上面是该吸管的包装状态(外侧绷紧),弯曲部分可视为一半圆环,设其外圆半径为xcm,则根据题意可列方程为6.5+2(10.5-6.5-x)+πx=15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com