
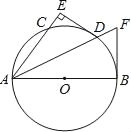
【题目】如图,AB为⊙O的直径,D是弧BC的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于F.
(1)求证:DE是⊙O的切线;
(2)若DE=3,⊙O的半径为5.求BF的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接BC、OD,由D是弧BC的中点,可知:OD⊥BC;由OB为⊙O的直径,可得:BC⊥AC,根据DE⊥AC,可证OD⊥DE,从而可证DE是⊙O的切线;
(2)在Rt△ABC中,运用勾股定理可求得AC的长度,运用切割线定理可将AE的长求出,根据△AED∽△ABF,可将BF的长求出.
试题解析:(1)证明:连接OD,BC,OD与BC相交于点G,
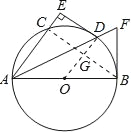
∵D是弧BC的中点,
∴OD垂直平分BC,
∵AB为⊙O的直径,
∴AC⊥BC,
∴OD∥AE.
∵DE⊥AC,
∴OD⊥DE,
∵OD为⊙O的半径,
∴DE是⊙O的切线.
(2)解:由(1)知:OD⊥BC,AC⊥BC,DE⊥AC,
∴四边形DECG为矩形,
∴CG=DE=3,
∴BC=6.
∵⊙O的半径为5,
∴AB=10,
∴AC=![]() =8,
=8,
由(1)知:DE为⊙O的切线,
∴DE2=ECEA,即32=(EA﹣8)EA,
解得:AE=9.
∵D为弧BC的中点,
∴∠EAD=∠FAB,
∵BF切⊙O于B,
∴∠FBA=90°.
又∵DE⊥AC于E,
∴∠E=90°,
∴∠FBA=∠E,
∴△AED∽△ABF,
∴![]() ,
,
∴![]() ,
,
∴BF=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
(1)请在图中作出△A′B′C′;(2)写出点A′、B′、C′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,AB=AC,点D、点O分别为BC、AC的中点,AE//BC.
(1)如图1,求证:四边形ADCE是矩形;
(2)如图2,若点 F是 CE上一动点,在不添加任何辅助线的情况下,请直接写出与四边形 ABDF 面积相等的三角形和四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2004年12月28日,我国第一条城际铁路正式开式建设,建成后,运行里程由目前的312千米缩短至154千米,设计时速是现行的2.5倍,施行列车运行时间将因此缩短3.13小时,求这条城际铁路的设计时速.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在四边形ABCD中,AD∥BC,AB∥DC,点E在BC延长线上,连接DE,∠A+∠E=180°.
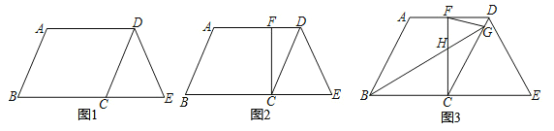
(1)如图1,求证:CD=DE;
(2)如图2,过点C作BE的垂线,交AD于点F,请直接写出BE、AF、DF 之间的数量关系_______________________;
(3)如图3,在(2)的条件下,∠ABC的平分线,交CD于G,交CF于H,连接FG,若∠FGH=45°,DF=8,CH=9,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减/吨 | ﹣1 | +3 | ﹣2 | +4 | +7 | ﹣5 | ﹣10 |
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )
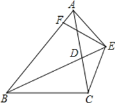
A.①②③B.①③④C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )

A. 4 B. 8 C. 10 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com