
°æƒø°ø![]() £®0£¨
£®0£¨ ![]() £©
£©![]() .
.
£®1£©«Û≈◊ŒÔœflµƒΩ‚Œˆ Ω.
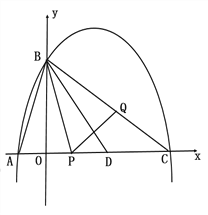
£®2£©≈◊ŒÔœfl”Î![]() ÷·Ωª”⁄¡Ì“ª∏ˆΩªµ„Œ™C£¨µ„D‘⁄œfl∂ŒAC…œ£¨“—÷™AD=AB£¨»Ù∂ص„P¥”A≥ˆ∑¢—ÿœfl∂ŒAC“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»‘»ÀŸ‘À∂Ø£¨Õ¨ ±¡Ì“ª∏ˆ∂ص„Q“‘ƒ≥“ªÀŸ∂»¥”B≥ˆ∑¢—ÿœfl∂ŒBC‘»ÀŸ‘À∂Ø£¨Œ «∑ҥʑ⁄ƒ≥“ª ±ø㨠πœfl∂ŒPQ±ª÷±œflBD¥π÷±∆Ω∑÷£¨»Ù¥Ê‘⁄£¨«Û≥ˆµ„Qµƒ‘À∂ØÀŸ∂»£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
÷·Ωª”⁄¡Ì“ª∏ˆΩªµ„Œ™C£¨µ„D‘⁄œfl∂ŒAC…œ£¨“—÷™AD=AB£¨»Ù∂ص„P¥”A≥ˆ∑¢—ÿœfl∂ŒAC“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»‘»ÀŸ‘À∂Ø£¨Õ¨ ±¡Ì“ª∏ˆ∂ص„Q“‘ƒ≥“ªÀŸ∂»¥”B≥ˆ∑¢—ÿœfl∂ŒBC‘»ÀŸ‘À∂Ø£¨Œ «∑ҥʑ⁄ƒ≥“ª ±ø㨠πœfl∂ŒPQ±ª÷±œflBD¥π÷±∆Ω∑÷£¨»Ù¥Ê‘⁄£¨«Û≥ˆµ„Qµƒ‘À∂ØÀŸ∂»£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
£®3£©‘⁄£®2£©µƒ«∞÷œ¬£¨π˝µ„Bµƒ÷±œfl![]() ”Î
”Î![]() ÷·µƒ∏∫∞Î÷·Ωª”⁄µ„M, «∑ҥʑ⁄µ„M, π“‘A°¢B°¢MŒ™∂•µ„µƒ»˝Ω«–Œ”Î
÷·µƒ∏∫∞Î÷·Ωª”⁄µ„M, «∑ҥʑ⁄µ„M, π“‘A°¢B°¢MŒ™∂•µ„µƒ»˝Ω«–Œ”Î![]() œ‡À∆,»Áπ˚¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆMµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
œ‡À∆,»Áπ˚¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆMµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”….
°æ¥∞∏°ø£®1£©![]() £ª£®2£©¥Ê‘⁄£¨µ„Qµƒ‘À∂ØÀŸ∂»√ø√Î
£ª£®2£©¥Ê‘⁄£¨µ„Qµƒ‘À∂ØÀŸ∂»√ø√Î![]() ∏ˆµ•Œª≥§∂»£ª£®3£©¥Ê‘⁄£¨
∏ˆµ•Œª≥§∂»£ª£®3£©¥Ê‘⁄£¨ ![]() £¨
£¨ ![]()
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©…Ë≈◊ŒÔœflµƒΩ‚Œˆ ΩŒ™y=a£®x-![]() £©2+k£®a°Ÿ0£©£¨∞—µ„A£®-1,0£©∫ÕB£®0£¨
£©2+k£®a°Ÿ0£©£¨∞—µ„A£®-1,0£©∫ÕB£®0£¨ ![]() £©¥˙»Î£¨Ω‚∑Ω≥ú¥ø…£ª
£©¥˙»Î£¨Ω‚∑Ω≥ú¥ø…£ª
£®2£© ◊œ»«Û≥ˆA°¢C◊¯±Í£¨”…°œDBP=°œDBQ£¨ø…µ√![]() £®Ω«∆Ω∑÷œflµƒ–‘÷ ∂®¿Ì£¨ø…“‘”√√ʪ˝∑®÷§√˜£©£¨º¥
£®Ω«∆Ω∑÷œflµƒ–‘÷ ∂®¿Ì£¨ø…“‘”√√ʪ˝∑®÷§√˜£©£¨º¥ £¨Ω‚∑Ω≥ú¥ø…£ª
£¨Ω‚∑Ω≥ú¥ø…£ª
£®3£©¥Ê‘⁄£¨¿Ì”…»Áœ¬£∫ ◊œ»÷§√˜°œBPC=°œBAM£¨∑÷¡Ω÷÷«ÈøˆÃ÷¬€£∫¢Ÿµ±![]() £¨°˜MAB°◊°˜BPC£¨¡–≥ˆ∑Ω≥ú¥ø…£ª¢⁄µ±
£¨°˜MAB°◊°˜BPC£¨¡–≥ˆ∑Ω≥ú¥ø…£ª¢⁄µ±![]() £¨°˜MAB°◊°˜CPB£¨¡–≥ˆ∑Ω≥ú¥ø….
£¨°˜MAB°◊°˜CPB£¨¡–≥ˆ∑Ω≥ú¥ø….
‘Ã‚Ω‚Œˆ£∫£®1£©![]()
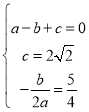
Ω‚µ√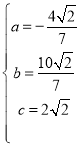
°‡![]()
£®2£©¡¨Ω”DQ,…Ët√Î ±£¨œfl∂ŒPQ±ª÷±œflBD¥π÷±∆Ω∑÷,
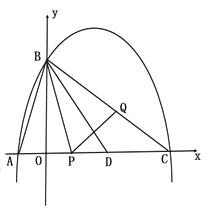
°fl![]()
![]() .
. ![]()
![]()
![]() =AD
=AD
‘Ú![]() ,CD=
,CD=![]()
°fl![]()
°‡![]()
°‡![]()
°‡![]()
°‡![]()
°‡![]()
°‡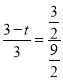
![]()
![]() ,OC=
,OC=![]() ,∏˘æ›π¥π…∂®¿Ìµ√£∫BC=
,∏˘æ›π¥π…∂®¿Ìµ√£∫BC=![]()
°‡![]()
°‡![]()
°‡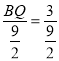
°‡![]()
![]() µ„Qµƒ‘À∂ØÀŸ∂»√ø√Î
µ„Qµƒ‘À∂ØÀŸ∂»√ø√Î![]() ∏ˆµ•Œª≥§∂»
∏ˆµ•Œª≥§∂»
£®3£©![]()
°‡![]()



| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
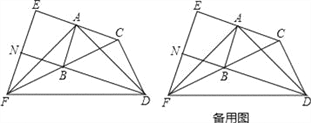
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC∫Õ°˜BCD÷–£¨°œBAC=°œBCD=90°„£¨AB=AC£¨CB=CD£Æ—”≥§CA÷¡µ„E£¨ πAE=AC£ª—”≥§CB÷¡µ„F£¨ πBF=BC£Æ¡¨Ω”AD£¨AF£¨DF£¨EF£Æ—”≥§DBΩªEF”⁄µ„N£Æ
£®1£©«Û÷§£∫AD=AF£ª
£®2£© ‘≈–∂œÀƒ±fl–ŒABNEµƒ–Œ◊¥£¨≤¢Àµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC∫Õ°˜DEC÷–£¨°œABC=°œDEC=90°„£¨¡¨Ω”ADΩª…‰œflEB”⁄F£¨π˝A◊˜AG°ŒDEΩª…‰œflEB”⁄µ„G£¨µ„F«°∫√ «AD÷–µ„°£
£®1£©«Û÷§£∫°˜AFG°’°˜DFE£ª
£®2£©»ÙBC=CE£¨¢Ÿ«Û÷§£∫°œABF=°œDEF£ª
¢⁄»Ù°œBAC=30°„£¨ ‘«Û°œAFGµƒ∂» ˝°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø ¬º˛°∞¥”µÿ√Ê∑¢…‰1√∂µºµØ,ª˜÷–ø’÷–ƒø±Í°± «____________ ¬º˛(ÃÓ°∞»∑∂®°±ªÚ°∞Àʪ˙°±)°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™ ![]() £¨
£¨ ![]() £¨
£¨
£®1£©µ± ![]() »°∫Œ÷µ ±£¨
»°∫Œ÷µ ±£¨ ![]() £ª
£ª
£®2£©µ± ![]() »°∫Œ÷µ ±£¨
»°∫Œ÷µ ±£¨ ![]() µƒ÷µ±»
µƒ÷µ±» ![]() µƒ÷µµƒ3±∂¥Û1£ª
µƒ÷µµƒ3±∂¥Û1£ª
£®3£©œ»Ãӱ̣¨∫Ûªÿ¥£∫
¢Ÿ
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| ||||||||
|
¢⁄∏˘æ›À˘ÃÓ±Ì∏Ò£¨ªÿ¥Œ £∫ÀÊ◊≈ ![]() µƒ÷µ‘ˆ¥Û£¨
µƒ÷µ‘ˆ¥Û£¨ ![]() µƒ÷µ÷Ω• £¨
µƒ÷µ÷Ω• £¨ ![]() µƒ÷µ÷Ω• £Æ
µƒ÷µ÷Ω• £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øΩ´»Ù∏…’≈≥§Œ™20¿Ô√Ê°¢øÌŒ™10¿Ô√ʵƒ≥§∑Ω–Œ∞◊÷Ω£¨∞¥ÕºÀ˘ 浃∑Ω∑®’≥∫œ∆¿¥£¨’≥∫œ≤ø∑÷µƒøÌŒ™2¿Â√◊£Æ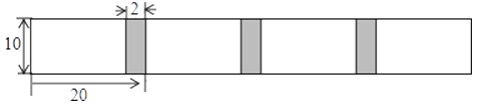
£®1£©«Û2’≈∞◊÷ΩÃ˘∫œ∫Ûµƒ◊‹≥§∂»£ªƒ«√¥3’≈∞◊÷Ω’≥∫œ∫Ûµƒ◊‹≥§∂»ƒÿ£ø4’≈ƒÿ£ø
£®2£©…Ëa’≈∞◊÷Ω’≥∫œ∫Ûµƒ◊‹≥§∂»Œ™b¿Ô√Ê£¨–¥≥ˆb”Îa÷ƺ‰µƒπÿœµ Ω£¨≤¢«Ûµ±a=100 ±£¨bµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº «º◊°¢““¡Ω»ÀÕ¨“ªµÿµ„≥ˆ∑¢∫Û£¨¬∑≥ÃÀÊ ±º‰±‰ªØµƒÕºœÛ£Æ
£®1£©¥À±‰ªØπ˝≥Ã÷–£¨ «◊‘±‰¡ø£¨ «“Ú±‰¡ø£Æ
£®2£©º◊µƒÀŸ∂» ““µƒÀŸ∂»£Æ£®¥Û”⁄°¢µ»”⁄°¢–°”⁄£©
£®3£©6 ±±Ì æ £ª
£®4£©¬∑≥ÃŒ™150km£¨º◊–– ª¡À –° ±£¨““–– ª¡À –° ±£Æ
£®5£©9 ±º◊‘⁄““µƒ £®«∞√Ê°¢∫Û√Ê°¢œ‡Õ¨Œª÷√£©
£®6£©““±»º◊œ»◊fl¡À3–° ±£¨∂‘¬£ø £Æ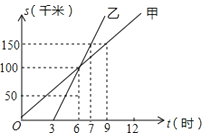
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫»ÁÕºÀ˘ 棨. l1°Œl2£¨°œ1+°œ2=180°„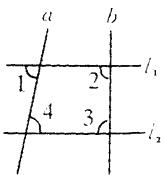
£®1£©«Û÷§£∫°œ1=°œ3.
£®2£©«Û°œ2+°œ4µƒ∂» ˝.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
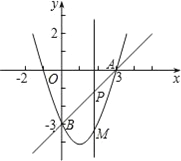
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨≈◊ŒÔœfly=x2+mx+næ≠π˝µ„A£®3£¨0£©°¢B£®0£¨©Å3£©£¨µ„P «÷±œflAB…œµƒ∂ص„£¨π˝µ„P◊˜x÷·µƒ¥πœflΩª≈◊ŒÔœfl”⁄µ„M£¨…˵„Pµƒ∫·◊¯±ÍŒ™t£Æ
£®1£©∑÷±«Û≥ˆ÷±œflAB∫Õ’‚Ãı≈◊ŒÔœflµƒΩ‚Œˆ Ω£Æ
£®2£©»Ùµ„P‘⁄µ⁄ÀƒœÛœfi£¨¡¨Ω”AM°¢BM£¨µ±œfl∂ŒPM◊Ó≥§ ±£¨«Û°˜ABMµƒ√ʪ˝£Æ
£®3£© «∑ҥʑ⁄’‚—˘µƒµ„P£¨ πµ√“‘µ„P°¢M°¢B°¢OŒ™∂•µ„µƒÀƒ±fl–ŒŒ™∆Ω––Àƒ±fl–Œ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆµ„Pµƒ∫·◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com