
【题目】如图是甲、乙两人同一地点出发后,路程随时间变化的图象.
(1)此变化过程中, 是自变量, 是因变量.
(2)甲的速度 乙的速度.(大于、等于、小于)
(3)6时表示 ;
(4)路程为150km,甲行驶了 小时,乙行驶了 小时.
(5)9时甲在乙的 (前面、后面、相同位置)
(6)乙比甲先走了3小时,对吗? .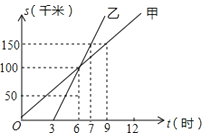
【答案】t;s;小于;乙追赶上了甲;9;4;后面;不对
【解析】解:(1)函数图象反映路程随时间变化的图象,则t是自变量,s为因变量;
(2)甲的速度=![]() =
=![]() 千米/小时,乙的速度=
千米/小时,乙的速度=![]() 千米/小时,所以甲的速度小于乙的速度;
千米/小时,所以甲的速度小于乙的速度;
(3)6时表示他们相遇,即乙追赶上了甲;
(4)路程为150km,甲行驶9小时;乙行驶了7﹣3=4小时;
(5)t=9时,乙的图象在甲的上方,即乙行驶的路程远些,所以9时甲在乙的后面
(6)不对,是乙比甲晚走了3小时.
所以答案是t,s;小于;乙追赶上了甲;9,4;后面;不对.
【考点精析】解答此题的关键在于理解函数的图象的相关知识,掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下列各关系中,符合正比例关系的是( )
A.正方形的周长P和它的一边长a
B.距离s一定时,速度v和时间t
C.圆的面积S和圆的半径r
D.正方体的体积V和棱长a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )
A.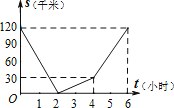
B.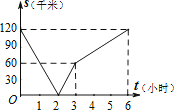
C.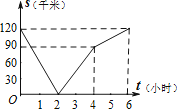
D.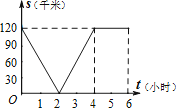
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() (0,
(0, ![]() )
)![]() .
.
(1)求抛物线的解析式.
(2)抛物线与![]() 轴交于另一个交点为C,点D在线段AC上,已知AD=AB,若动点P从A出发沿线段AC以每秒1个单位长度的速度匀速运动,同时另一个动点Q以某一速度从B出发沿线段BC匀速运动,问是否存在某一时刻,使线段PQ被直线BD垂直平分,若存在,求出点Q的运动速度;若不存在,请说明理由.
轴交于另一个交点为C,点D在线段AC上,已知AD=AB,若动点P从A出发沿线段AC以每秒1个单位长度的速度匀速运动,同时另一个动点Q以某一速度从B出发沿线段BC匀速运动,问是否存在某一时刻,使线段PQ被直线BD垂直平分,若存在,求出点Q的运动速度;若不存在,请说明理由.
(3)在(2)的前提下,过点B的直线![]() 与
与![]() 轴的负半轴交于点M,是否存在点M,使以A、B、M为顶点的三角形与
轴的负半轴交于点M,是否存在点M,使以A、B、M为顶点的三角形与![]() 相似,如果存在,请直接写出M的坐标;若不存在,请说明理由.
相似,如果存在,请直接写出M的坐标;若不存在,请说明理由.
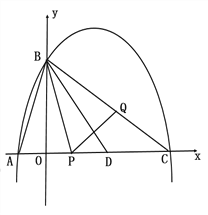
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某初中每天早上总是在规定时间打开学校大门,七年级同学小明每天早上同一时间从家到学校,周一早上他骑自行车以每小时12千米的速度到校,结果在校门口等了6分钟才开门,周二早上他步行以每小时6千米的速度到校,结果校门已开了12分钟,请解决以下问题:
(1)小明从家到学校的路程是多少千米?
(2)周三早上小明想准时到达学校门口,那么他应以每小时多少千米度速度到学校?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知xm=2,xn=3,求x2m+3n的值;
(2)先化简,再求值:(a+2b)(a-2b)+(a+2b)2+(2ab2-8a2b2)÷2ab,其中a=1,b=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角梯形ABCD中,∠A=∠D=90°,DC<AB,AB=AD=12,E是边AD上的一点,恰好使CE=10,并且∠CBE=45°,则AE的长是( )
A.2或8
B.4或6
C.5
D.3或7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算(-8m4n+12m3n2-4m2n3)÷(-4m2n) 的结果是( )
A. 2m2n-3m+n2 B. 2m2-3nm2+n2
C. 2m2-3mn+n D. 2m2-3mn+n2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com