
【题目】已知,A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )
A.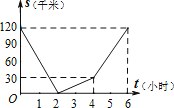
B.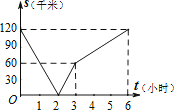
C.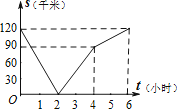
D.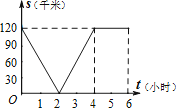
【答案】B
【解析】解:根据题意,两人同时相向出发,甲到达B地时间为:![]() =6小时,乙到达A地:
=6小时,乙到达A地:![]() =3小时.
=3小时.
根据题意,分成两个阶段:相遇前、相遇后;相遇后可分成乙到达A地、甲到达B地;
相遇前,s=120﹣(20+40)t=120﹣60t(0≤t≤2),当两者相遇时,t=2,s=0,
相遇后,当乙到达A地前,甲乙均在行驶,即s=(20+40)(t﹣2)=60t﹣120(2≤t≤3),当乙到达A地时,此时两者相距60千米;
当乙到达A地后,剩下甲在行驶,即s=60+20(t﹣3)=20t(3≤t≤6),
故:
法二:本题可无需列出方程,只需弄清楚题意,分清楚s与t的变化可分为几个阶段:相遇前、相遇后;相遇后可分成乙到达A地、甲到达B地,故求出各个时间点便可.
∵A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A,
∴两人同时出发,2小时两人就会相遇,甲6小时到达B地,乙3小时到达A地,
故两人之间的距离为s(千米),甲行驶的时间为t(小时),则正确反映s与t之间函数关系的是B.
故选:B.
根据题意求出2小时两人就会相遇,甲6小时到达B地,乙3小时到达A地,进而根据相遇前、相遇后两个阶段得出相应的分段函数,从而找出符合题意的图象.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】如图反映的过程是:小强从家去菜地浇水,又去玉米地除草,然后回家.如果菜地和玉米地的距离为a千米,小强在玉米地除草比在菜地浇水多用的时间为b分钟,则a,b的值分别为( )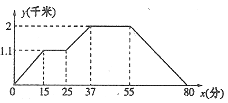
A.1.1,8
B.0.9,3
C.1.1,12
D.0.9,8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,∠ABC=∠DEC=90°,连接AD交射线EB于F,过A作AG∥DE交射线EB于点G,点F恰好是AD中点。
(1)求证:△AFG≌△DFE;
(2)若BC=CE,①求证:∠ABF=∠DEF;
②若∠BAC=30°,试求∠AFG的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(﹣ 2,﹣ 2),(![]() ,
, ![]() ),…,都是梦之点,显然梦之点有无数个.
),…,都是梦之点,显然梦之点有无数个.
(1)若点 P(2,b)是反比例函数![]() (n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(2)⊙ O 的半径是![]() ,
,

①求出⊙ O 上的所有梦之点的坐标;
②已知点 M(m,3),点 Q 是(1)中反比例函数![]() 图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,tan∠OAQ= 1.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,tan∠OAQ= 1.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 ![]() ,
, ![]() ,
,
(1)当 ![]() 取何值时,
取何值时, ![]() ;
;
(2)当 ![]() 取何值时,
取何值时, ![]() 的值比
的值比 ![]() 的值的3倍大1;
的值的3倍大1;
(3)先填表,后回答:
①
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| ||||||||
|
②根据所填表格,回答问题:随着 ![]() 的值增大,
的值增大, ![]() 的值逐渐 ,
的值逐渐 , ![]() 的值逐渐 .
的值逐渐 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两人同一地点出发后,路程随时间变化的图象.
(1)此变化过程中, 是自变量, 是因变量.
(2)甲的速度 乙的速度.(大于、等于、小于)
(3)6时表示 ;
(4)路程为150km,甲行驶了 小时,乙行驶了 小时.
(5)9时甲在乙的 (前面、后面、相同位置)
(6)乙比甲先走了3小时,对吗? .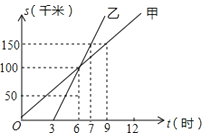
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中生在数学运算中使用计算器的现象越来越普遍,某校一兴趣小组随机抽查了本校若干名学生使用计算器的情况.以下是根据抽查结果绘制出的不完整的条形统计图和扇形统计图:
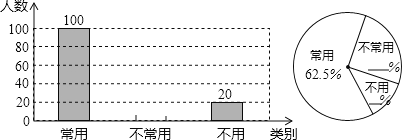
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是 ;
(2)请补全上述条形统计图和扇形统计图;
(3)若从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com