
【题目】直角梯形ABCD中,∠A=∠D=90°,DC<AB,AB=AD=12,E是边AD上的一点,恰好使CE=10,并且∠CBE=45°,则AE的长是( )
A.2或8
B.4或6
C.5
D.3或7
【答案】B
【解析】解:如图,过点B作BF⊥CD交DC的延长线于F,
∵∠A=∠D=90°,AB=AD,
∴四边形ABFD是正方形,
把△ABE绕点B顺时针旋转90°得到△BFG,
则AE=FG,BE=BG,∠ABE=∠FBG,
∵∠CBE=45°,
∴∠CBG=∠CBF+∠FBG=∠CBF+∠ABE=90°﹣∠CBE=90°﹣45°=45°,
∴∠CBE=∠CBG,
在△CBE和△CBG中,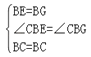
∴△CBE≌△CBG(SAS),
∴CE=CG,
∴AE+CF=FG+CF=CG=CE,
设AE=x,则DE=12﹣x,CF=10﹣x,
∴CD=12﹣(10﹣x)=x+2,
在Rt△CDE中,CD2+DE2=CE2 ,
即(x+2)2+(12﹣x)2=102 ,
整理得,x2﹣10x+24=0,
解得x1=4,x2=6,
所以AE的长是4或6.
故选B.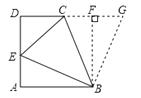


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,∠ABC=∠DEC=90°,连接AD交射线EB于F,过A作AG∥DE交射线EB于点G,点F恰好是AD中点。
(1)求证:△AFG≌△DFE;
(2)若BC=CE,①求证:∠ABF=∠DEF;
②若∠BAC=30°,试求∠AFG的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两人同一地点出发后,路程随时间变化的图象.
(1)此变化过程中, 是自变量, 是因变量.
(2)甲的速度 乙的速度.(大于、等于、小于)
(3)6时表示 ;
(4)路程为150km,甲行驶了 小时,乙行驶了 小时.
(5)9时甲在乙的 (前面、后面、相同位置)
(6)乙比甲先走了3小时,对吗? .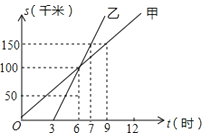
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣ ![]() ×(0.5﹣
×(0.5﹣ ![]() )÷(﹣
)÷(﹣ ![]() )
)
(2)﹣22﹣[(﹣3)×(﹣ ![]() )﹣(﹣2)3]
)﹣(﹣2)3]
(3)当x=2,y= ![]() 时,化简求值:
时,化简求值: ![]() x﹣(﹣
x﹣(﹣ ![]() )﹣(2x﹣
)﹣(2x﹣ ![]() y2)
y2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张长方形的餐桌可以坐6个人,按照下图的方式摆放餐桌和椅子:
(1)观察表中数据规律填表:
餐桌张数 | 1 | 2 | 3 | 4 | …n |
可坐人数 | 6 | 8 | 10 |
(2)一家酒楼,按上图的方式拼桌,要使拼成的一张大餐桌刚好能坐160人,请问需几张餐桌拼成一张大餐桌?
(3)若酒店有240人来就餐,哪种拼桌的方式更好?最少要用多少张餐桌?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中生在数学运算中使用计算器的现象越来越普遍,某校一兴趣小组随机抽查了本校若干名学生使用计算器的情况.以下是根据抽查结果绘制出的不完整的条形统计图和扇形统计图:
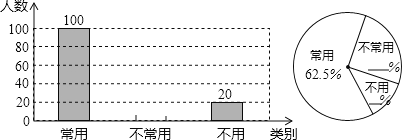
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是 ;
(2)请补全上述条形统计图和扇形统计图;
(3)若从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
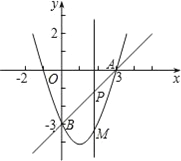
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、B(0,﹣3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.
(1)分别求出直线AB和这条抛物线的解析式.
(2)若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.
(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请求出点P的横坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com