
【题目】附加题:如图,已知∠1=∠2,∠3=∠4,∠A=100°,求x的值. 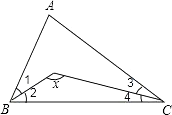
【答案】解:∵在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=100°, ∴∠ABC+∠ACB=180°﹣100°=80°,
∵∠1=∠2,∠3=∠4,
∴∠2+∠4= ![]() (∠ABC+∠ACB)=40°,
(∠ABC+∠ACB)=40°,
∴x=180°﹣(∠2+∠4)=140°.
【解析】根据的是三角形内角和定理以及角平分线性质解答即可.
【考点精析】认真审题,首先需要了解角的平分线(从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线),还要掌握三角形的内角和外角(三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角)的相关知识才是答题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校20名同学去工厂进行暑假实践活动,每名同学每天可以加工甲种零件5个或乙种零件4个,已知每加工一个甲种零件可获利16元,每加工一个乙种零件可获利24元,若要使车间每天获利不低于1 800元,至少要派( )名同学加工乙种零件.
A. 11 B. 12 C. 13 D. 14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈![]() ,tan48°≈
,tan48°≈![]() ,sin64°≈
,sin64°≈![]() ,tan64°≈2)
,tan64°≈2)
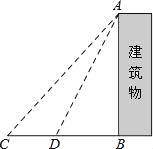
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内),其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2).
(1)当点C落在边EF上时,x=_____cm;
(2)若两个三角板重叠部分的图形为四边形时,求y关于x的函数解析式,并写出自变量x的取值范围;
(3)设边BC的中点为点M,边DF的中点为点N,直接写出在三角板平移过程中,点M与点N之间距离的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com