
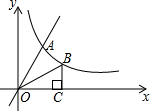
 如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图形上任意一点(不与点A重合),BC⊥x轴于点C.
如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图形上任意一点(不与点A重合),BC⊥x轴于点C.分析 (1)由直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),先将A(1,a)代入直线y=2x求出a的值,从而确定A点的坐标,然后将A点的坐标代入反比例函数y=$\frac{k}{x}$中即可求出k的值;
(2)由反比例函数y=$\frac{k}{x}$的比例系数k的几何意义,可知△BOC的面积等于$\frac{1}{2}$|k|,从而求出△OBC的面积.
解答 解:(1)∵直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),先
∴将A(1,a)代入直线y=2x,得:
a=2
∴A(1,2),
将A(1,2)代入反比例函数y=$\frac{k}{x}$中得:k=2,
∴y=$\frac{2}{x}$;
(2)∵B是反比例函数y=$\frac{k}{x}$图象上的点,且BC⊥x轴于点C,
∴△BOC的面积=$\frac{1}{2}$|k|=$\frac{1}{2}$×2=1.
点评 本题主要考查函数图象的交点及待定系数法求函数解析式,掌握图象的交点的坐标满足两个函数解析式是解题的关键.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:解答题
 正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图.
正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
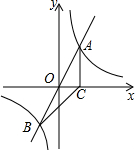 如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
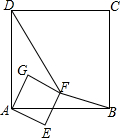
 如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽△BEF;④S△BEF=$\frac{72}{5}$.在以上4个结论中,正确的有( )
如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽△BEF;④S△BEF=$\frac{72}{5}$.在以上4个结论中,正确的有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
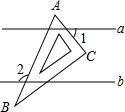 如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为( )
如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为( )| A. | 105° | B. | 110° | C. | 115° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com