
如图,点E、F、G、H分别在菱形ABCD的四条边上,且BE=BF=DG=DH,连接EF,FG,GH,HE得到四边形EFGH.
(1)求证:四边形EFGH是矩形;
(2)设AB=a,∠A=60°,当BE为何值时,矩形EFGH的面积最大?

【考点】菱形的性质;二次函数的最值;矩形的判定与性质.
【分析】(1)利用等腰三角形的性质:等边对等角,以及平行线的性质可以证得∠DGH+∠CGH=90°,则∠HGF=90°,根据三个角是直角的四边形是矩形,即可证得;
(2)设BE的长是x,则利用x表示出矩形EFGH的面积,根据函数的性质即可求解.
【解答】(1)证明:∵DG=DH,
∴∠DHG=∠DGH=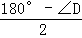 ,
,
同理,∠CGF=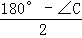 ,
,
∴∠DGH+∠CGF=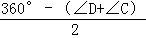 ,
,
又∵菱形ABCD中,AD∥BC,
∴∠D+∠C=180°,
∴∠DGH+∠CGF=90°,
∴∠HGF=90°,
同理,∠GHE=90°,∠EFG=90°,
∴四边形EFGH是矩形;
(2)AB=a,∠A=60°,则菱形ABCD的面积是: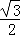 a2,
a2,
设BE=x,则AE=a﹣x,
则△AEH的面积是: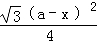 ,
,
△BEF的面积是: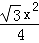 ,
,
则矩形EFGH的面积y=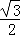 a2﹣
a2﹣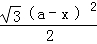 ﹣
﹣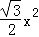 ,
,
即y=﹣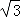 x2+
x2+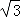 ax,
ax,
则当x=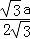 =
=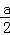 时,函数有最大值.
时,函数有最大值.
此时BE=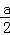 .
.
【点评】本题考查了菱形的性质,矩形的判定以及二次函数的性质,正确利用x表示出矩形EFGH的面积是关键.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
有理数a、b在数轴上表示的点如图,则a、﹣a、b、﹣b大小关系是( )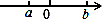
A.﹣b>a>﹣a>b B.a>﹣a>b>﹣b C.b>a>﹣b>﹣a D.﹣b<a<﹣a<b
查看答案和解析>>
科目:初中数学 来源: 题型:
每天供给地球光和热的太阳与我们的距离非常遥远,它距地球的距离约为15000000千米,将150000000千米用科学记数法表示为( )
A.0.15×109千米 B.1.5×108千米 C.15×107千米 D.1.5×107千米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com