
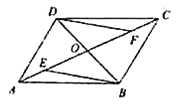
【题目】如图,![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 是
是![]() 上的两点,并且
上的两点,并且![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证![]() ;
;
(2)若![]() ,连接
,连接![]() ,
,![]() ,判断四边形
,判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)详见解析;(2)四边形BEDF是矩形,理由详见解析.
【解析】
(1)已知四边形ABCD是平行四边形,根据平行四边形的性质可得OA=OC,OB=OD,由AE=CF即可得OE=OF,利用SAS证明△BOE≌△DOF, 根据全等三角形的性质即可得BE=DF;(2)四边形BEDF是矩形.由(1)得OD=OB,OE=OF, 根据对角线互相平方的四边形为平行四边形可得四边形BEDF是平行四边形, 再由BD=EF,根据对角线相等的平行四边形为矩形即可判定四边形EBFD是矩形.
(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OE=OF,
在△BOE和△DOF中,
 ,
,
∴△BOE≌△DOF(SAS),
∴BE=DF;
(2)四边形BEDF是矩形.理由如下:
如图所示:
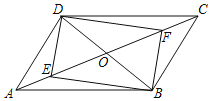
∵OD=OB,OE=OF,
∴四边形BEDF是平行四边形,
∵BD=EF,
∴四边形EBFD是矩形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送![]() 批客人,行驶路程记录如下(规定向东为正,向西为负,单位:
批客人,行驶路程记录如下(规定向东为正,向西为负,单位:![]() ):
):
第 | 第 | 第 | 第 | 第 |
|
|
|
|
|
(1)接送完第![]() 批客人后,该驾驶员在公司什么方向,距离公司多少千米?
批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油![]() 升,那么在这过程中共耗油多少升?
升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过![]() 收费
收费![]() 元,超过
元,超过![]() 的部分按每千米
的部分按每千米![]() 元收费,在这过程中该驾驶员共收到车费多少元?
元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y= x2+bx+c与x轴、y轴分别相交于点A( 1,0)、B(0,3)两点,其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短。若存在请求出P点的坐标,若不存在说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=150,∠AOC=40,OE是∠AOB内部的一条射线,OF平分∠AOE, 且OF在OC的右侧.
(1)若∠EOB=10,求∠COF的度数;
(2)若∠COF=20,求∠EOB的度数;
(3)若∠COF=n,求∠EOB的度数(用含n的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店老板第一次用1000元购进一批文具,很快销售完毕,第二次购进时发现每件文具的进价比第一次上涨了2.5元,老板用2500元购进了第二批文具,所购进文具的数量是第一次购进数量的2倍,同样很快销售完毕,已知两批文具的售价均为每件15元.
(1)第二次购进了多少件文具?
(2)文具店老板在这两笔生意中共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线过原点O,点A(10,0)和点B(2,2),在线段OA上,点P从点O向点A运动,同时点Q从点A向点O运动,运动过程中保持AQ=2OP,当P、Q重合时同时停止运动,过点Q作x轴的垂线,交直线AB于点M,延长QM到点D,使MD=MQ,以QD为对角线作正方形QCDE(正方形QCDE随点Q运动).
(1)求这条抛物线的函数表达式;
(2)设正方形QCDE的面积为S,P点坐标(m,0)求S与m之间的函数关系式;
(3)过点P作x轴的垂线,交抛物线于点N,延长PN到点G,使NG=PN,以PG为对角线作正方形PFGH(正方形PFGH随点P运动),当点P运动到点(2,0)时,如图2,正方形PFGH的边GF和正方形QCDE的边EQ落在同一条直线上.
①则此时两个正方形中在直线AB下方的阴影部分面积的和是多少?
②若点P继续向点A运动,还存在两个正方形分别有边落在同一条直线上的情况,请直接写出每种情况下点P的坐标,不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家文化用品商场平时以同样价格出售相同的商品.六一期间两家商场都让利酬宾,其中甲商场所有商品一律按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.
(1)分别写出两家商场购物金额![]() (元)与商品原价
(元)与商品原价![]() (元)的函数解析式;
(元)的函数解析式;
(2)在如图所示的直角坐标系中画出(1)中函数的图象;
(3)六一期间如何选择这两家商场购物更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业500名员工参加安全生产知识测试,成绩记为A,B,C,D,E共5个等级,为了解本次测试的成绩(等级)情况,现从中随机抽取部分员工的成绩(等级),统计整理并制作了如下的统计图:
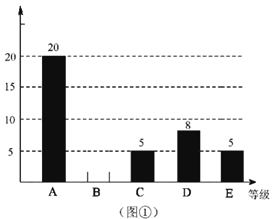
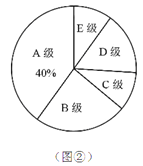
(1)求这次抽样调查的样本容量,并补全图①;
(2)如果测试成绩(等级)为A,B,C级的定为优秀,请估计该企业参加本次安全生产知识测试成绩(等级)达到优秀的员工的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块三角形空地上种草皮绿化,已知AB=20米,AC=30米,∠A=150°,草皮的售价为a元/米2,则购买草皮至少需要( )
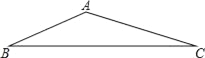
A. 450a元 B. 225a元 C. 150a元 D. 300a元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com