
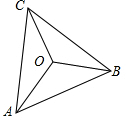
 如图,点O是等边三角形ABC内一点,已知∠AOB=115°,∠BOC=125°,则在以线段OA,OB,OC为边构成的三角形中,内角不可能取到的角度是( )
如图,点O是等边三角形ABC内一点,已知∠AOB=115°,∠BOC=125°,则在以线段OA,OB,OC为边构成的三角形中,内角不可能取到的角度是( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
分析 可通过旋转将△AOB旋转至△BDC,则可得△BOD是等边三角形,把OA,OB,OC放在一个三角形中,进而求出各个角的大小.
解答 解:如图所示,将△AOB旋转至△BDC,则BO=BD,∠ABO=∠CBD,
∴∠ABO+∠CBO=∠CBD+∠CBO,
即∠ABC=∠OBD=60°,
∴△BOD是等边三角形,所以OD=OB=BD,
又可证得OA=DC,故以线段OA、OB、OC为三边所形成的三角形为△OCD,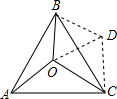
∵∠AOB=115°,∠BOC=120°,
∴∠BDC=115°,
又∵∠BDO=60°,
∴∠ODC=55°
∵∠BOC=120°,∠DOB=60°,
∴∠DOC=60°,
∴∠OCD=65°,
∴三角形三内角的度数分别为65°、55°、60°.
故选D.
点评 本题考查了旋转的性质,全等三角形的性质,等边三角形的判定和性质,掌握等边三角形的性质,能够通过旋转的方法巧妙地求解是解题的关键.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:解答题
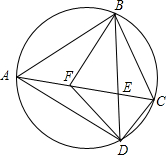 如图,已知四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC.
如图,已知四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
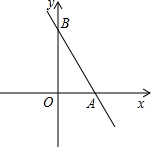 直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B,M是y轴上一点,若将△ABM沿AM折叠,点B恰好落在x轴上,则点M的坐标为(0,$\frac{3}{2}$)或(0,-6).
直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B,M是y轴上一点,若将△ABM沿AM折叠,点B恰好落在x轴上,则点M的坐标为(0,$\frac{3}{2}$)或(0,-6).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
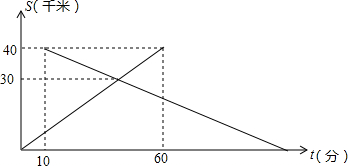
| A. | 14:00 | B. | 14:20 | C. | 14:30 | D. | 14:40 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某通讯公司推出了①②两种收费方式,收费y1,y2 (元)与通讯时间x(分钟)之间的函数关系如图所示,则使不等式kx+30<$\frac{1}{5}$x成立的x的取值范围是x>300.
某通讯公司推出了①②两种收费方式,收费y1,y2 (元)与通讯时间x(分钟)之间的函数关系如图所示,则使不等式kx+30<$\frac{1}{5}$x成立的x的取值范围是x>300.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
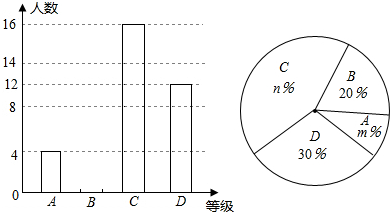
| A. | 参加演讲比赛学生共40人 | |
| B. | 扇形统计图中m=10,n=40 | |
| C. | 学校欲从获A等级的学生中随机选取2人参加市级比赛,选中A等级的小明的概率为$\frac{1}{2}$ | |
| D. | C等级所对应的圆心角为120度 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
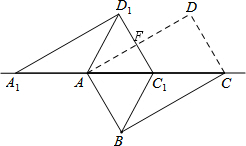 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1、BC1.
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1、BC1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com