
【题目】观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…,按此规律第6个图中共有点的个数是( )
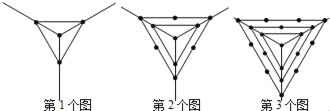
A.46B.63C.64D.73
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:如图(1),在四边形ABCD中,若AB=AD,BC=CD,则把这样的四边形称之为筝形.
(1)写出筝形的两个性质(定义除外).
① ;② .
(2)如图(2),在平行四边形ABCD中,点E、F分别在BC、CD上,且AE=AF,∠AEC=∠AFC.求证:四边形AECF是筝形.
(3)如图(3),在筝形ABCD中,AB=AD=26,BC=DC=25,AC=17,求筝形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(模型建立)
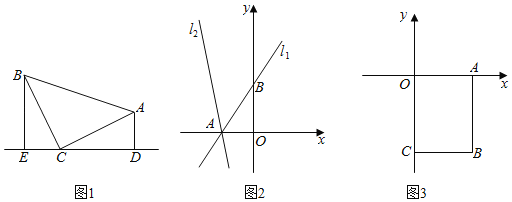
(1)如图1,等腰Rt△ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E,求证:△BEC≌△CDA;
(模型应用)
(2)如图2,已知直线l1:y=![]() x+3与x轴交于点A,与y轴交于点B,将直线l1绕点A逆时针旋转45°至直线l2;求直线l2的函数表达式;
x+3与x轴交于点A,与y轴交于点B,将直线l1绕点A逆时针旋转45°至直线l2;求直线l2的函数表达式;
(3)如图3,平面直角坐标系内有一点B(3,﹣4),过点B作BA⊥x轴于点A、BC⊥y轴于点C,点P是线段AB上的动点,点D是直线y=﹣2x+1上的动点且在第四象限内.试探究△CPD能否成为等腰直角三角形?若能,求出点D的坐标,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
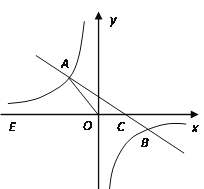
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(- 3,4),点B的坐标为(6,n).
的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(- 3,4),点B的坐标为(6,n).
(1)求该反比例函数和一次函数的解析式;
(2)连接OB,求△AOB 的面积;
(3)在x轴上是否存在点P,使△APC是直角三角形. 若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
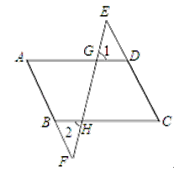
【题目】如图,在四边形ABCD中,E、F分别是CD、AB延长线上的点,连结EF,分别交AD、BC于点G、H.若∠1=∠2,∠A=∠C,试说明AD∥BC和AB∥CD.
请完成下面的推理过程,并填空(理由或数学式):
∵∠1=∠2( )
∠1=∠AGH( )
∴∠2=∠AGH( )
∴AD∥BC( )
∴∠ADE=∠C( )
∵∠A=∠C( )
∴∠ADE=∠A
∴AB∥CD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCF中,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD,EA,延长EA交CD于点G.
(1)求证:△ACE≌△CBD;
(2)求∠CGE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
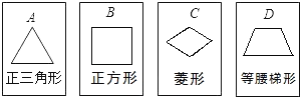
【题目】有四张背面相同的纸牌A,B,C,D,其正面分别划有四个不同的几何图形(如图).小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.
(1)用树状图(或列表法)表示两次模牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张牌面图形既是中心对称图形又是轴对称图形的纸牌的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处.
⑴若∠PEF=48°,点Q恰好落在其中的一条平行线上,则∠EFP的度数为 .
⑵若∠PEF=75°,∠CFQ=![]() ∠PFC,求∠EFP的度数.
∠PFC,求∠EFP的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com