
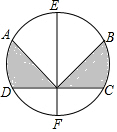
 如图A,B,C,D,E,F把半径为3厘米的圆6等分,则阴影部分的面积为( )
如图A,B,C,D,E,F把半径为3厘米的圆6等分,则阴影部分的面积为( )| A. | 9π | B. | 3π | C. | 6π | D. | $\frac{9}{4}$π |
分析 先设EF的中点为O,则O为圆心,连接OA,OB,OC,OD,再判定△BOC是等边三角形,得出∠BOE=∠OBC,BC=BO=CO=3,进而得到BC∥EF,可得△BCG面积=△BCO面积,故扇形BOC的面积=EF右边阴影部分的面积,根据EF右边阴影部分的面积=$\frac{3}{2}π$,可得图中阴影部分的面积.
解答 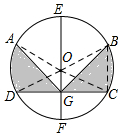 解:设EF的中点为O,则O为圆心,
解:设EF的中点为O,则O为圆心,
连接OA,OB,OC,OD,
∵A,B,C,D,E,F把半径为3厘米的圆6等分,
∴∠EOB=∠BOC=∠CPF=60°,
又∵OB=OC,
∴△BOC是等边三角形,
∴∠BOE=∠OBC,BC=BO=CO=3,
∴BC∥EF,
∴△BCG面积=△BCO面积,
∴扇形BOC的面积=EF右边阴影部分的面积,
又∵扇形BOC的面积=$\frac{60×π×{3}^{2}}{360}$=$\frac{3}{2}π$,
∴EF右边阴影部分的面积=$\frac{3}{2}π$,
同理可得,EF左边阴影部分的面积=$\frac{3}{2}π$,
∴阴影部分的面积为3π.
故选:B.
点评 本题主要考查了扇形面积以及等边三角形的性质的运用,解决问题的关键是掌握:由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:选择题
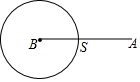 如图,动点S从点A出发,沿线段AB运动至点B后,立即按原路返回,点S在运动过程中速度不变,则以点B为圆心,线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为( )
如图,动点S从点A出发,沿线段AB运动至点B后,立即按原路返回,点S在运动过程中速度不变,则以点B为圆心,线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为( )| A. |  | B. |  | C. | 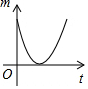 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{10}{x}$-$\frac{10}{2x}$=15 | B. | $\frac{10}{2x}$-$\frac{10}{x}$=15 | C. | $\frac{10}{x}$-$\frac{10}{2x}$=$\frac{1}{4}$ | D. | $\frac{10}{2x}$-$\frac{10}{x}$=$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 最高分 | B. | 中位数 | C. | 极差 | D. | 平均数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
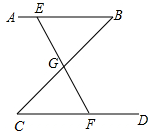 如图,公园里有一条“Z”形的林荫小道ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一条石凳E、G、F,且G恰好为BC的中点,E、G、F三点在同一条直线上,点G与F之间有一座假山,而使得两处不能直接到达.你能想出测量G、F之间距离的方法吗?说明其中的道理.
如图,公园里有一条“Z”形的林荫小道ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一条石凳E、G、F,且G恰好为BC的中点,E、G、F三点在同一条直线上,点G与F之间有一座假山,而使得两处不能直接到达.你能想出测量G、F之间距离的方法吗?说明其中的道理.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 到C地 | 到D地 | |
| A果园 | 每吨15元 | 每吨12元 |
| B果园 | 每吨10元 | 每吨9元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
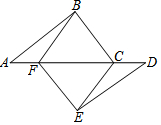 如图,点A、F、C、D在同一条直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠BAD=∠ADE,AF=DC.求证:四边形BCEF是平行四边形.
如图,点A、F、C、D在同一条直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠BAD=∠ADE,AF=DC.求证:四边形BCEF是平行四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com