
| ��C�� | ��D�� | |
| A�� | ÿ��15Ԫ | ÿ��12Ԫ |
| B�� | ÿ��10Ԫ | ÿ��9Ԫ |
���� ��1����A����ƻ��������ϴ�A���˵�C�ص�ƻ���������ɵó���A���˵�D�ص�ƻ���������ٸ����˷�=�����������˷Ѽ��ɵó����ۣ�
��2������C��D������Ҫ��ƻ���������ɵó���B���˵�C��D����ƻ�����������ٸ������˷�=A��ƻ���˳����ܷ���+B��ƻ���˳������˷Ѽ��ɵó����ۣ�
��3�����ݣ�2���Ľ��۽�����˷Ѽ��ɵó�����x��һԪһ�η��̣���֮���ɵó����ۣ�
��� �⣺��1����A����ƻ��30�֣���A���˵�C�ص�ƻ��Ϊx�֣�
���A���˵�D�ص�ƻ��Ϊ��30-x���֣�
���A����ƻ������D�ص��������Ϊ12��30-x��Ԫ��
�ʴ�Ϊ��30-x��12��30-x����
��2����C��D���طֱ���Ҫƻ��25�ֺ�45�֣�
���B���˵�C�ص�ƻ��Ϊ��25-x���֣���B���˵�D�ص�ƻ��Ϊ45-��30-x��=��15+x���֣�
���������=15x+12��30-x��+10��25-x��+9��15+x��=2x+745��
��3����������ã�2x+745=785��
��ã�x=20��
������������Ϊ785Ԫʱ����ô��A���˵�C�ص�ƻ��Ϊ20�֣�
���� ���⿼����һԪһ�η��̵�Ӧ���Լ��д���������Ĺؼ��ǣ���1������������ϵA��ƻ��������=A������C��ƻ������+A������D��ƻ�������г�����ʽ����2������������ϵ���˷�=A��ƻ���˳����ܷ���+B��ƻ���˳������˷��г�����ʽ����3����ϣ�2�������Լ����˷��г�����x��һԪһ�η��̣�


 Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д� �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ������a��b�������ϵĶ�Ӧ��λ����ͼ��ʾ�������н�����ȷ���ǣ�������
������a��b�������ϵĶ�Ӧ��λ����ͼ��ʾ�������н�����ȷ���ǣ�������| A�� | a+b��0 | B�� | a-b=0 | C�� | a+b��0 | D�� | a-b��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
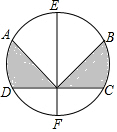 ��ͼA��B��C��D��E��F�Ѱ뾶Ϊ3����Բ6�ȷ֣�����Ӱ���ֵ����Ϊ��������
��ͼA��B��C��D��E��F�Ѱ뾶Ϊ3����Բ6�ȷ֣�����Ӱ���ֵ����Ϊ��������| A�� | 9�� | B�� | 3�� | C�� | 6�� | D�� | $\frac{9}{4}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{3}$ | B�� | 3 | C�� | 1��-2 | D�� | $\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x | 3 | 5 | 7 |
| y | 0.08 | 0.08 | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
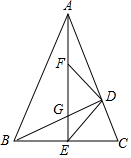 ��֪����ͼ���ڡ�ABC�У���BAC=45�㣬BD��AE�ֱ��DZ�AC��BC���ϵĸߣ�AE��BD���ڵ�G����E����F�ֱ���BC��AG���е㣮�жϡ�DEF����״����˵�����ɣ�
��֪����ͼ���ڡ�ABC�У���BAC=45�㣬BD��AE�ֱ��DZ�AC��BC���ϵĸߣ�AE��BD���ڵ�G����E����F�ֱ���BC��AG���е㣮�жϡ�DEF����״����˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
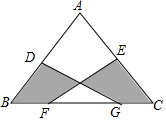 ��ͼ���ڡ�ABC�У�AB=AC=10��BC=12��D��E�ֱ�ΪAB��AC�е㣬F��GΪ�߶�BC�����㣬��FG=6������Ӱ�������Ϊ24��
��ͼ���ڡ�ABC�У�AB=AC=10��BC=12��D��E�ֱ�ΪAB��AC�е㣬F��GΪ�߶�BC�����㣬��FG=6������Ӱ�������Ϊ24���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com