
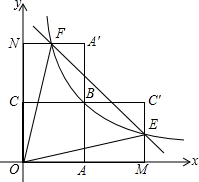
 如图,四边形OABC是面积为4的正方形,反比例函数y=
如图,四边形OABC是面积为4的正方形,反比例函数y=| k |
| x |
| k |
| x |
| k |
| x |
| 81 |
| 4 |
| 81 |
| 4 |
| k |
| x |
| k |
| x |
| k |
| x |
| 4 |
| x |
|
|
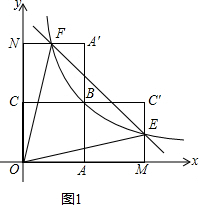
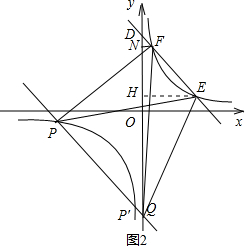 过点P作PQ∥EF交y轴于点Q,连接QE、QF,
过点P作PQ∥EF交y轴于点Q,连接QE、QF,| 81 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 81 |
| 4 |
| 27 |
| 2 |
| 27 |
| 2 |
| 17 |
| 2 |
| 17 |
| 2 |
|
|
|
| 1 |
| 2 |
| 1 |
| 2 |
|
|


科目:初中数学 来源: 题型:
 (1)如图,在Rt△ABC中,∠C=90°,BD是三角形的角平分线,交AC于点D,AD=2.2cm,AC=3.7cm,则点D到AB边的距离是
(1)如图,在Rt△ABC中,∠C=90°,BD是三角形的角平分线,交AC于点D,AD=2.2cm,AC=3.7cm,则点D到AB边的距离是查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
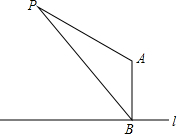 随着科学技术的不断进步,我国海上能源开发和利用已达到国际领先水平.下图为我国在南海海域自主研制的海上能源开发的机器装置AB,一直升飞机在离海平面l距离为150米的空中点P处,看到该机器顶部点A处的俯角为38°,看到露出海平面的机器部分点B处的俯角为65°,求这个机器装置露出海平面部分AB的高度?(结果精确到0.1,参考数据:sin65°=0.9063,sin38°=0.6157,tan38°=0.7813,tan65°=2.1445.)
随着科学技术的不断进步,我国海上能源开发和利用已达到国际领先水平.下图为我国在南海海域自主研制的海上能源开发的机器装置AB,一直升飞机在离海平面l距离为150米的空中点P处,看到该机器顶部点A处的俯角为38°,看到露出海平面的机器部分点B处的俯角为65°,求这个机器装置露出海平面部分AB的高度?(结果精确到0.1,参考数据:sin65°=0.9063,sin38°=0.6157,tan38°=0.7813,tan65°=2.1445.)查看答案和解析>>
科目:初中数学 来源: 题型:
| A、2.5×106米 |
| B、2.5×105米 |
| C、2.5×10-6米 |
| D、2.5×10-5米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com