
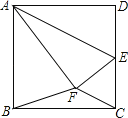
【题目】如图,已知正方形ABCD的边长为4,点E为边DC的中点,连结AE,将△ADE沿着AE翻折,使点D落在正方形内的点F处,连结BF、CF,则S△BFC的面积为 .
【答案】![]()
【解析】
试题分析:根据题意得出S△ADE+S△AFE+S△EFC+S△ABF+S△BFC=4×4,进而得出S△BFC=FN,再利用勾股定理得出FN的长,进而得出答案.
解:∵正方形ABCD的边长为4,点E为边DC的中点,连结AE,将△ADE沿着AE翻折,使点D落在正方形内的点F处,
∴△ADE≌△AFE,DE=EC=EF=2,AB=AF=4,
过点F作FN⊥CD于点N,FM⊥AB于点M,
∴S△ADE+S△AFE+S△EFC+S△ABF+S△BFC=4×4,
∴![]() ×2×4+
×2×4+![]() ×2×4+
×2×4+![]() ×2×FN+
×2×FN+![]() ×4×(4﹣FN)+S△BFC=16,
×4×(4﹣FN)+S△BFC=16,
∴8+FN+8﹣2FN+S△BFC=16,
∴S△BFC=FN=![]() ×BC×NC=2NC,
×BC×NC=2NC,
设NC=x,则FN=2x,EN=2﹣x,
∴EF2=EN2+FN2,
∴22=(2﹣x)2+(2x)2,
解得:x1=0(不合题意舍去),x2=![]() ,
,
∴FN=2×![]() =
=![]() ,
,
∴S△BFC=![]() .
.
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
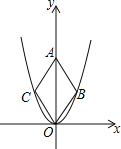
【题目】二次函数y=![]() x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=
x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=![]() x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于被墨水污染,一道几何题仅能见到如图所示的图形和文字:“如图,已知:四边形ABCD中,AD∥BC,∠D=67°,…”
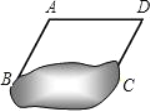
(1)根据以上信息,你可以求出∠A、∠B、∠C中的哪个角?写出求解的过程;
(2)若要求出其它的角,请你添上一个适当的条件: ,并写出解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明所在城市的“阶梯水价”收费办法是:每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨加收2元,小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )
A. 5x+4(x+2)=44 B. 5x+4(x﹣2)=44 C. 9(x+2)=44 D. 9(x+2)﹣4×2=44
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与小华本学期都参加了5次数学考试(总分均为100分),数学老师想判断这两位同学的数学成绩谁更稳定,在作统计分析时,老师需比较这两人5次数学成绩的( )
A. 平均数 B. 方差 C. 众数 D. 中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果线段AB=13cm,MA+MB=17 cm,那么下面说法中正确的是 ( ).
A. M点在线段AB上 B. M点在直线AB上
C. M点在直线AB外 D. M点可能在直线AB上,也可能在直线AB外
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com