
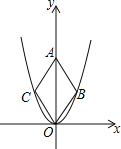
【题目】二次函数y=![]() x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=
x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=![]() x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
【答案】2![]()
【解析】
试题分析:连结BC交OA于D,如图,根据菱形的性质得BC⊥OA,∠OBD=60°,利用含30度的直角三角形三边的关系得OD=![]() BD,设BD=t,则OD=
BD,设BD=t,则OD=![]() t,B(t,
t,B(t,![]() t),利用二次函数图象上点的坐标特征得
t),利用二次函数图象上点的坐标特征得![]() t2=
t2=![]() t,解得t1=0(舍去),t2=1,则BD=1,OD=
t,解得t1=0(舍去),t2=1,则BD=1,OD=![]() ,然后根据菱形性质得BC=2BD=2,OA=2OD=2
,然后根据菱形性质得BC=2BD=2,OA=2OD=2![]() ,再利用菱形面积公式计算即可.
,再利用菱形面积公式计算即可.
解:连结BC交OA于D,如图,
∵四边形OBAC为菱形,
∴BC⊥OA,
∵∠OBA=120°,
∴∠OBD=60°,
∴OD=![]() BD,
BD,
设BD=t,则OD=![]() t,
t,
∴B(t,![]() t),
t),
把B(t,![]() t)代入y=
t)代入y=![]() x2得
x2得![]() t2=
t2=![]() t,解得t1=0(舍去),t2=1,
t,解得t1=0(舍去),t2=1,
∴BD=1,OD=![]() ,
,
∴BC=2BD=2,OA=2OD=2![]() ,
,
∴菱形OBAC的面积=![]() ×2×2
×2×2![]() =2
=2![]() .
.
故答案为2![]() .
.


科目:初中数学 来源: 题型:
【题目】在△ABC和△A′B′C中,∠A=∠A′,CD与C′D′分别为AB边和A′B′边上的中线,再从以下三个条件:①AB=A′B′;②AC=A′C′;③CD=C′D′中任取两个为题设,另一个作为结论,请写出一个正确的命题:________(用题序号写).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,采取分段收费.若每户每月用水不超过20m3,每立方米收费2元;若用水超过20m3,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水 m3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列填空.如右图,已知AD⊥BC,EF⊥BC,∠1=∠2. 求证: DG∥BA.

证明:∵AD⊥BC,EF⊥BC(已知)
∴∠EFB=∠ADB=90° ( )
∴ ∥ ( )
∴∠1=∠BAD ( )
又∵∠1=∠2 (已知)
∴ (等量代换)
∴DG∥BA. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AB∥DC,AB=16cm,CD=10cm,AD=5cm DE⊥AB,垂足为E,点P从点A出发,以2cm/秒的速度沿AB向终点B运动;点Q从点C出发,以1cm/秒的速度沿CD向终点D运动(P,Q两点中,有一个点运动到终点时,所有运动即终止),设P,Q同时出发并运动了t秒.

(1)当四边形EPQD为矩形时,求t的值.
(2)当以点E、P、C、Q为顶点的四边形是平行四边形时,求t的值;
(3)探索:是否存在这样的t值,使三角形PDQ是以PD为腰的等腰三角形?若存在,求出t的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
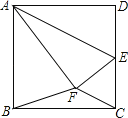
【题目】如图,已知正方形ABCD的边长为4,点E为边DC的中点,连结AE,将△ADE沿着AE翻折,使点D落在正方形内的点F处,连结BF、CF,则S△BFC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中有2个红球、3个绿球和5个白球,这些球除颜色外都相同,将球搅匀,从中任意摸出1个球.
(1)会出现哪些可能的结果? ;
(2)你认为摸到哪种颜色球的可能性最大? ;
(3)怎样改变袋子中红球和白球的个数,使摸到这两种颜色球的概率相同?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com