
【题目】一只不透明的袋子中有2个红球、3个绿球和5个白球,这些球除颜色外都相同,将球搅匀,从中任意摸出1个球.
(1)会出现哪些可能的结果? ;
(2)你认为摸到哪种颜色球的可能性最大? ;
(3)怎样改变袋子中红球和白球的个数,使摸到这两种颜色球的概率相同?
【答案】(1)摸到红球,摸到绿球,摸到白球;(2)白球(3)放入3个红球;放入2个红球,拿走1个白球等
【解析】
试题分析:(1)由一只不透明的袋子中有2个红球、3个绿球和5个白球,即可求得答案;
(2)由一只不透明的袋子中有2个红球、3个绿球和5个白球,这些球除颜色外都相同,即可求得摸到各种颜色球的概率,继而求得答案;
(3)使得袋子中红球和白球的个数相等即可.
解:(1)∵一只不透明的袋子中有2个红球、3个绿球和5个白球,
∴会出现3种结果:摸到红球,摸到绿球,摸到白球;
故答案为:会出现3种结果:摸到红球,摸到绿球,摸到白球;
(2)∵一只不透明的袋子中有2个红球、3个绿球和5个白球,这些球除颜色外都相同,
∴P(红球)=![]() =
=![]() ,P(绿球)=
,P(绿球)=![]() ,P(白球)=
,P(白球)=![]() =
=![]() ,
,
∴摸到白球的可能性最大.
故答案为:白球;
(3)答案不唯一如:放入3个红球;放入2个红球,拿走1个白球等.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
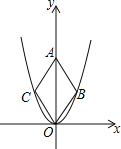
【题目】二次函数y=![]() x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=
x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=![]() x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果线段AB=13cm,MA+MB=17 cm,那么下面说法中正确的是 ( ).
A. M点在线段AB上 B. M点在直线AB上
C. M点在直线AB外 D. M点可能在直线AB上,也可能在直线AB外
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课外兴趣小组活动时,老师提出了如下问题:
(1)如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:
延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.

感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形或全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)问题解决:
受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(3)问题拓展:
如图3,在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作∠EDF为60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地去年财政收入取得重大突破,地方公共财政收入用四舍五入取近似值后为27.39亿元,那么这个数值( )
A. 精确到亿位 B. 精确到百分位
C. 精确到千万位 D. 精确到百万位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com