
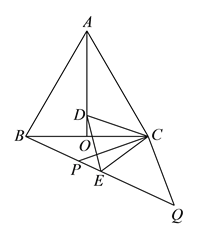
【题目】如图,等边![]() 中,
中, ![]() 是
是![]() 的角平分线,
的角平分线, ![]() 为
为![]() 上一点,以
上一点,以![]() 为一边且在
为一边且在![]() 下方作等边
下方作等边![]() ,连接
,连接![]() .
.
(![]() )求证:
)求证: ![]() ≌
≌![]() .
.
(![]() )延长
)延长![]() 至
至![]() ,
, ![]() 为
为![]() 上一点,连接
上一点,连接![]() 、
、![]() 使
使![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
【答案】(![]() )证明见解析;(
)证明见解析;(![]() )PQ=8.
)PQ=8.
【解析】试题分析:
(1)由△ABC、△DCE都是等边三角形可得:AC=BC、CD=CE,∠ACB=∠DCE=60°,从而可得∠ACD=∠BCE,这样由“SAS”即可证得:△ACD≌△BCE;
(2)由等边△ABC中,AO平分∠BAC可得∠CAD=![]() ∠BAC=30°,结合△ACD≌△BCE可得∠CBE=30°;过点C作CH⊥BQ于点H,由此可得CH=
∠BAC=30°,结合△ACD≌△BCE可得∠CBE=30°;过点C作CH⊥BQ于点H,由此可得CH=![]() BC=3,在Rt△CHQ中,由勾股定理可得HQ=4,结合CP=CQ可得PQ=2HQ=8.
BC=3,在Rt△CHQ中,由勾股定理可得HQ=4,结合CP=CQ可得PQ=2HQ=8.
试题解析:
(![]() )∵
)∵![]() ,
, ![]() 均为等边三角形,
均为等边三角形,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
在![]() 和
和![]() 中,
中,
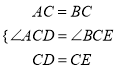 ,
,
∴![]() ≌
≌![]() .
.
(![]() )∵等边△ABC中,AO平分∠BAC,
)∵等边△ABC中,AO平分∠BAC,
∴∠CAD=![]() ∠BAC=30°.
∠BAC=30°.
如下图,过![]() 点作
点作![]() ,垂足为
,垂足为![]() ,
,
由(![]() )知
)知![]() ≌
≌![]() ,
,
则![]() ,
,
∴![]() ,
,
∴在![]() 中,
中, ![]() ,
,
又∵CP=CQ,CH⊥PQ,
∴![]() .
.



科目:初中数学 来源: 题型:
【题目】(本题10分)如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=![]() ,DE=3.
,DE=3.

求:(1)⊙O的半径;(2)弦AC的长;(3)阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下一组勾股数:________.
(2)若第一个数用字母n(n为奇数,且n≥3)表示,那么后两个数用含n的代数式分别表示为________和________,请用所学知识说明它们是一组勾股数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(![]() )在
)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰三角形,求出点
为等腰三角形,求出点![]() 坐标.
坐标.
(![]() )在
)在![]() 轴上方存在点
轴上方存在点![]() ,使以点
,使以点![]() ,
, ![]() ,
, ![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,画出
全等,画出![]() 并请直接写出点
并请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年级261位学生参加期末考试,某班35位学生的语文成绩、数学成绩与总成绩在全年级中的排名情况如图1和图2所示,甲、乙、丙为该班三位学生.

从这次考试成绩看,
① 在甲、乙两人中,总成绩名次靠前的学生是_________;
② 在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是国外城市与北京的时差(带正号的数表示同一时刻比北京时间早的时数).那么与北京时间最接近的城市是( )
城市 | 伦敦 | 墨尔本 | 东京 | 巴黎 |
时差(时) | ﹣8 | +3 | +1 | ﹣7 |
A.伦敦B.墨尔本C.东京D.巴黎
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com