
ШчЭМЃЌвбжЊЖўДЮКЏЪ§ЕФЭМЯѓЙ§ЕуOЃЈ0ЃЌ0ЃЉЃЌAЃЈ4ЃЌ0ЃЉЃЌBЃЈ2ЃЌЉ ЃЉЃЌMЪЧOAЕФжаЕуЃЎ
ЃЉЃЌMЪЧOAЕФжаЕуЃЎ
ЃЈ1ЃЉЧѓДЫЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшPЪЧХзЮяЯпЩЯЕФвЛЕуЃЌЙ§PзїxжсЕФЦНааЯпгыХзЮяЯпНЛгкСэвЛЕуQЃЌвЊЪЙЫФБпаЮPQAMЪЧСтаЮЃЌЧѓPЕуЕФзјБъЃЛ
ЃЈ3ЃЉНЋХзЮяЯпдкxжсЯТЗНЕФВПЗжбиxжсЯђЩЯЗелЃЌЕУЧњЯпOBЁфAЃЈBЁфЮЊBЙигкxжсЕФЖдГЦЕуЃЉЃЌдкдХзЮяЯпxжсЕФЩЯЗНВПЗжШЁвЛЕуCЃЌСЌНгCMЃЌCMгыЗелКѓЕФЧњЯпOBЁфAНЛгкЕуDЃЎШєЁїCDAЕФУцЛ§ЪЧЁїMDAУцЛ§ЕФ2БЖЃЌетбљЕФЕуCЪЧЗёДцдкЃПШєДцдкЧѓГіCЕуЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

(1) y=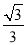 x2Љ
x2Љ xЃЎ(2) PЃЈ1ЃЌЉ
xЃЎ(2) PЃЈ1ЃЌЉ ЃЉЃЎ(3) ЕуCЕФзјБъЮЊЃЈ2+2
ЃЉЃЎ(3) ЕуCЕФзјБъЮЊЃЈ2+2 ЃЌ
ЃЌ ЃЉЛђЃЈ2Љ2
ЃЉЛђЃЈ2Љ2 ЃЌ
ЃЌ ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉгЩЫФБпаЮPQAMЪЧСтаЮЃЌПЩжЊPQ=2ЧвPQЁЮxжсЃЌвђДЫЕуPЁЂQЙигкЖдГЦжсx=2ЖдГЦЃЌПЩЕУЕуPКсзјБъЮЊ1ЃЌДгЖјЧѓГіЕуPЕФзјБъЃЛ
ЃЈ3ЃЉМйЩшДцдкТњзуЬѕМўЕФЕуCЃЎгЩЁїCDAЕФУцЛ§ЪЧЁїMDAУцЛ§ЕФ2БЖЃЌПЩЕУЕуCзнзјБъЪЧЕуDзнзјБъЕФ3БЖЃЌгЩДЫСаЗНГЬЧѓГіЕуCЕФзјБъЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпХзЮяЯпЙ§дЕуЃЌЁрЩшЦфНтЮіЪНЮЊЃКy=ax2+bxЃЎ
ЁпХзЮяЯпОЙ§ЕуAЃЈ4ЃЌ0ЃЉЃЌBЃЈ2ЃЌЉ ЃЉЃЌ
ЃЉЃЌ
Ёр ЃЌНтЕУ
ЃЌНтЕУ ЃЌ
ЃЌ
ЁрЖўДЮКЏЪ§НтЮіЪНЮЊЃКy=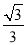 x2Љ
x2Љ xЃЎ
xЃЎ
ЃЈ2ЃЉЁпy=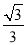 x2Љ
x2Љ x=
x=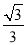 ЃЈxЉ2ЃЉ2Љ
ЃЈxЉ2ЃЉ2Љ ЃЌ
ЃЌ
ЁрХзЮяЯпЖдГЦжсЮЊжБЯпЃКx=2ЃЎ
ЁпЫФБпаЮPQAMЪЧСтаЮЃЌ
ЁрPQ=MA=2ЃЌPQЁЮxжсЃЎ
ЁрЕуPЁЂQЙигкЖдГЦжсx=2ЖдГЦЃЌ
ЁрЕуPКсзјБъЮЊ1ЃЎ
ЕБx=1ЪБЃЌy=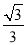 Љ
Љ =Љ
=Љ ЃЎ
ЃЎ
ЁрPЃЈ1ЃЌЉ ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉвРЬтвтЃЌЗелжЎКѓЕФХзЮяЯпНтЮіЪНЮЊЃКy=Љ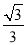 x2+
x2+ xЃЎ
xЃЎ
МйЩшДцдкетбљЕФЕуCЃЌ
ЁпЁїCDAЕФУцЛ§ЪЧЁїMDAУцЛ§ЕФ2БЖЃЌ
ЁрCD=2MDЃЌЁрCM=3MDЃЎ
ШчЭМЫљЪОЃЌЗжБ№Й§ЕуDЁЂCзїxжсЕФДЙЯпЃЌДЙзуЗжБ№ЮЊЕуEЁЂЕуFЃЌдђгаDEЁЮCFЃЎ

Ёр ЃЌ
ЃЌ
ЁрCF=3DEЃЌMF=3MEЃЎ
ЩшCЃЈxЃЌ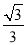 x2Љ
x2Љ xЃЉЃЌ
xЃЉЃЌ
дђMF=xЉ2ЃЌME=MF=ЃЈxЉ2ЃЉЃЌOE=ME+OM=x+
ЁрDЃЈx+ЃЌЉ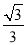 ЃЈx+ЃЉ2+
ЃЈx+ЃЉ2+ ЃЈx+ЃЉЃЉЃЎ
ЃЈx+ЃЉЃЉЃЎ
ЁпCF=3DEЃЌ
Ёр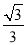 x2Љ
x2Љ x=3[Љ
x=3[Љ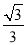 ЃЈx+ЃЉ2+
ЃЈx+ЃЉ2+ ЃЈx+ЃЉ]ЃЌ
ЃЈx+ЃЉ]ЃЌ
ећРэЕУЃКx2Љ4xЉ8=0ЃЌ
НтЕУЃКx1=2+2 ЃЌx2=2Љ2
ЃЌx2=2Љ2 ЃЎ
ЃЎ
Ёрy1= ЃЌy2=
ЃЌy2= ЃЌ
ЃЌ
ЁрДцдкТњзуЬѕМўЕФЕуCЃЌЕуCЕФзјБъЮЊЃЈ2+2 ЃЌ
ЃЌ ЃЉЛђЃЈ2Љ2
ЃЉЛђЃЈ2Љ2 ЃЌ
ЃЌ ЃЉЃЎ
ЃЉЃЎ
ПМЕуЃКЖўДЮКЏЪ§злКЯЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯЯцЬЖОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
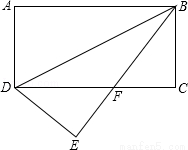
ШчЭМЃЌНЋОиаЮABCDбиBDЖделЃЌЕуAТфдкEДІЃЌBEгыCDЯрНЛгкFЃЌШєAD=3ЃЌBD=6ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїEDFЁеЁїCBFЃЛ
ЃЈ2ЃЉЧѓЁЯEBCЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯгРжнОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
ФГаЁ7УћГѕжаФаЩњВЮМгв§ЬхЯђЩЯЬхг§ВтЪдЕФГЩМЈЗжБ№ЮЊЃК8ЃЌ5ЃЌ7ЃЌ5ЃЌ8ЃЌ6ЃЌ8ЃЌдђетзщЪ§ОнЕФжкЪ§КЭжаЮЛЪ§ЗжБ№ЮЊЃЈЁЁЁЁЃЉ
AЃЎ6ЃЌ7 BЃЎ8ЃЌ7 CЃЎ8ЃЌ6 DЃЎ5ЃЌ7
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯжъжоОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
ШчЭМЃЌЕуAЁЂBЁЂCЖМдкдВOЩЯЃЌШчЙћЁЯAOB+ЁЯACB=84ЁуЃЌФЧУДЁЯACBЕФДѓаЁЪЧЁЁ ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯжъжоОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
вбжЊЗДБШР§КЏЪ§y= ЕФЭМЯѓОЙ§ЕуЃЈ2ЃЌ3ЃЉЃЌФЧУДЯТСаЫФИіЕужаЃЌвВдкетИіКЏЪ§ЭМЯѓЩЯЕФЪЧЃЈЁЁЁЁЃЉ
ЕФЭМЯѓОЙ§ЕуЃЈ2ЃЌ3ЃЉЃЌФЧУДЯТСаЫФИіЕужаЃЌвВдкетИіКЏЪ§ЭМЯѓЩЯЕФЪЧЃЈЁЁЁЁЃЉ
AЃЎЃЈЉ6ЃЌ1ЃЉ BЃЎЃЈ1ЃЌ6ЃЉ CЃЎЃЈ2ЃЌЉ3ЃЉ DЃЎЃЈ3ЃЌЉ2ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯГЃЕТОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
аЁУРжмФЉРДЕНЙЋдАЃЌЗЂЯждкЙЋдАвЛНЧгавЛжжЁАЪижъД§ЭУЁБгЮЯЗЃЎгЮЯЗЩшМЦепЬсЙЉСЫвЛжЛЭУзгКЭвЛИігаAЁЂBЁЂCЁЂDЁЂEЮхИіГіШыПкЕФЭУС§ЃЌЖјЧвС§ФкЕФЭУзгДгУПИіГіШыПкзпГіЭУС§ЕФЛњЛсЪЧОљЕШЕФЃЎЙцЖЈЃК
ЂйЭцМвжЛФмНЋаЁЭУДгAЁЂBСНИіГіШыПкЗХШыЃЛ
ЂкШчЙћаЁЭУНјШыС§згКѓбЁдёДгПЊЪМНјШыЕФГіШыПкРыПЊЃЌдђПЩЛёЕУвЛжЛМлжЕ5дЊаЁЭУЭцОпЃЌЗёдђгІИЖЗб3дЊЃЎ
ЃЈ1ЃЉЮЪаЁУРЕУЕНаЁЭУЭцОпЕФЛњЛсгаЖрДѓЃП
ЃЈ2ЃЉМйЩшга100ШЫДЮЭцДЫгЮЯЗЃЌЙРМЦгЮЯЗЩшМЦепПЩзЌЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯГЃЕТОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
вЛдЊЖўДЮЗНГЬ2x2Љ3x+k=0гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌдђkЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯдРбєОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
ФГЯюЧђРрБШШќЃЌУПГЁБШШќБиаыЗжГіЪЄИКЃЌЦфжаЪЄ1ГЁЕУ2ЗжЃЌИК1ГЁЕУ1ЗжЃЎФГЖгдкШЋВП16ГЁБШШќжаЕУЕН25ЗжЃЌЧѓетИіЖгЪЄЁЂИКГЁЪ§ЗжБ№ЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯТІЕзОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
ШєСНдВЕФАыОЖЗжБ№ЮЊ2cmКЭ6cmЃЌдВаФОрЮЊСЫ8cmЃЌдђСНдВЕФЮЛжУЙиЯЕЮЊЃЈЁЁЁЁЃЉ
AЃЎЭтЧа BЃЎЯрНЛ CЃЎФкЧа DЃЎЭтРы
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com