
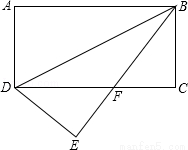
如图,将矩形ABCD沿BD对折,点A落在E处,BE与CD相交于F,若AD=3,BD=6.
(1)求证:△EDF≌△CBF;
(2)求∠EBC.
(1)证明见解析
(2)∠EBC=30°.
【解析】
试题分析:(1)由矩形的性质和折叠的性质可得DE=BC,∠E=∠C=90°,对顶角∠DFE=∠BFC,利用AAS可判定△DEF≌△BCF;
(2)由已知知△ABD是直角三角形,由已知AD=3,BD=6,可得出∠ABD=30°,然后利用折叠的性质可得∠DBE=30°,继而可求得∠EBC的度数.
试题解析:(1)由折叠的性质可得:DE=BC,∠E=∠C=90°,
在△DEF和△BCF中,
 ,
,
∴△DEF≌△BCF(AAS);
(2)在Rt△ABD中,
∵AD=3,BD=6,
∴∠ABD=30°,
由折叠的性质可得;∠DBE=∠ABD=30°,
∴∠EBC=90°﹣30°﹣30°=30°.
考点:1、矩形的性质;2、全等三角形的判定与性质;3、图形的翻折


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源:2014年初中毕业升学考试(湖南衡阳卷)数学(解析版) 题型:解答题
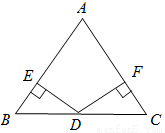
如图,在△ABC中,AB=AC,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F.
求证:△BED≌△CFD.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南湘潭卷)数学(解析版) 题型:解答题
△ABC为等边三角形,边长为a,DF⊥AB,EF⊥AC,
(1)求证:△BDF∽△CEF;
(2)若a=4,设BF=m,四边形ADFE面积为S,求出S与m之间的函数关系,并探究当m为何值时S取最大值;
(3)已知A、D、F、E四点共圆,已知tan∠EDF= ,求此圆直径.
,求此圆直径.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南湘潭卷)数学(解析版) 题型:填空题
七、八年级学生分别到雷锋、毛泽东纪念馆参观,共589人,到毛泽东纪念馆的人数是到雷锋纪念馆人数的2倍多56人.设到雷锋纪念馆的人数为x人,可列方程为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南湘潭卷)数学(解析版) 题型:选择题
如图,A、B两点在双曲线y=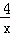 上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=( )
上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=( )

A.3 B.4 C.5 D.6
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南永州卷)数学(解析版) 题型:填空题
小聪,小玲,小红三人参加“普法知识竞赛”,其中前5题是选择题,每题10分,每题有A、B两个选项,且只有一个选项是正确的,三人的答案和得分如下表,试问:这五道题的正确答案(按1~5题的顺序排列)是
题号 答案 选手 | 1 | 2 | 3 | 4 | 5 | 得分 |
小聪 | B | A | A | B | A | 40 |
小玲 | B | A | B | A | A | 40 |
小红 | A | B | B | B | A | 30 |
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南常德卷)数学(解析版) 题型:解答题
如图,已知二次函数的图象过点O(0,0),A(4,0),B(2,﹣ ),M是OA的中点.
),M是OA的中点.
(1)求此二次函数的解析式;
(2)设P是抛物线上的一点,过P作x轴的平行线与抛物线交于另一点Q,要使四边形PQAM是菱形,求P点的坐标;
(3)将抛物线在x轴下方的部分沿x轴向上翻折,得曲线OB′A(B′为B关于x轴的对称点),在原抛物线x轴的上方部分取一点C,连接CM,CM与翻折后的曲线OB′A交于点D.若△CDA的面积是△MDA面积的2倍,这样的点C是否存在?若存在求出C点的坐标,若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com