
△ABC为等边三角形,边长为a,DF⊥AB,EF⊥AC,
(1)求证:△BDF∽△CEF;
(2)若a=4,设BF=m,四边形ADFE面积为S,求出S与m之间的函数关系,并探究当m为何值时S取最大值;
(3)已知A、D、F、E四点共圆,已知tan∠EDF= ,求此圆直径.
,求此圆直径.

(1)证明见解析
(2)S与m之间的函数关系为:S═﹣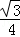 (m﹣2)2+3
(m﹣2)2+3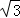 (其中0<m<4).当m=2时,S取到最大值,最大值为3
(其中0<m<4).当m=2时,S取到最大值,最大值为3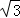
(3)此圆直径长为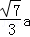 .
.
【解析】
试题分析:(1)由已知可知∠BDF=∠CEF,∠B=∠C,所以得证.
(2)四边形ADFE面积S可以看成△ADF与△AEF的面积之和,这两个三角形均为直角三角形,在△BDF与△CEF中,由三角函数可以用m表示出BD、DF、CE、EF的长,进而可得AD、AE的长,从而可以用含m的代数式表示S,然后通过配方,转化为二次函数的最值问题,就可以解决问题.
(3)由已知易知AF就是圆的直径,利用圆周角定理将∠EDF转化为∠EAF.在△AFC中,知道tan∠EAF、∠C、AC,通过解直角三角形就可求出AF长.
试题解析:(1):∵DF⊥AB,EF⊥AC,
∴∠BDF=∠CEF=90°.
∵△ABC为等边三角形,
∴∠B=∠C=60°.
∵∠BDF=∠CEF,∠B=∠C,
∴△BDF∽△CEF.
(2)∵∠BDF=90°,∠B=60°,
∴sin60°=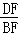 =
=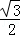 ,cos60°=
,cos60°= =
=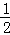 .
.
∵BF=m,
∴DF=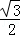 m,BD=
m,BD=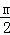 .
.
∵AB=4,
∴AD=4﹣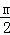 .
.
∴S△ADF=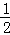 AD•DF
AD•DF
=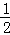 ×(4﹣
×(4﹣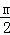 )×
)×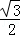 m
m
=﹣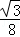 m2+
m2+ m.
m.
同理:S△AEF=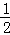 AE•EF
AE•EF
=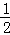 ×(4﹣
×(4﹣ )×
)×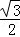 (4﹣m)
(4﹣m)
=﹣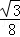 m2+2
m2+2 .
.
∴S=S△ADF+S△AEF
=﹣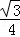 m2+
m2+ m+2
m+2
=﹣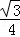 (m2﹣4m﹣8)
(m2﹣4m﹣8)
=﹣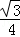 (m﹣2)2+3
(m﹣2)2+3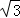 .其中0<m<4.
.其中0<m<4.
∵﹣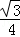 <0,0<2<4,
<0,0<2<4,
∴当m=2时,S取最大值,最大值为3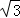 .
.
∴S与m之间的函数关系为:
S═﹣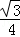 (m﹣2)2+3
(m﹣2)2+3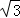 (其中0<m<4).
(其中0<m<4).
当m=2时,S取到最大值,最大值为3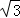 .
.
(3)如图2,
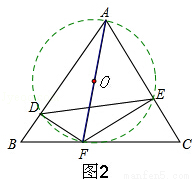
∵A、D、F、E四点共圆,
∴∠EDF=∠EAF.
∵∠ADF=∠AEF=90°,
∴AF是此圆的直径.
∵tan∠EDF=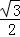 ,
,
∴tan∠EAF=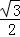 .
.
∴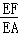 =
=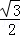 .
.
∵∠C=60°,
∴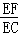 =tan60°=
=tan60°=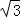 .
.
设EC=x,则EF=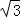 x,EA=2x.
x,EA=2x.
∵AC=a,
∴2x+x=a.
∴x=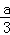 .
.
∴EF= ,AE=
,AE=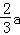 .
.
∵∠AEF=90°,
∴AF=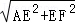 =
=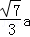 .
.
∴此圆直径长为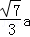 .
.
考点:1、相似三角形;2、二次函数的最值;3、三角函数;4、解直角三角形


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014年初中毕业升学考试(湖南衡阳卷)数学(解析版) 题型:解答题
二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点为A(﹣3,0)、B(1,0)两点,与y轴交于点C(0,﹣3m)(其中m>0),顶点为D.
(1)求该二次函数的解析式(系数用含m的代数式表示);
(2)如图①,当m=2时,点P为第三象限内的抛物线上的一个动点,设△APC的面积为S,试求出S与点P的横坐标x之间的函数关系式及S的最大值;
(3)如图②,当m取何值时,以A、D、C为顶点的三角形与△BOC相似?

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南衡阳卷)数学(解析版) 题型:选择题
若一个多边形的内角和是900°,则这个多边形的边数是( )
A.5 B.6 C.7 D.8
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南湘潭卷)数学(解析版) 题型:解答题
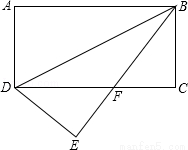
如图,将矩形ABCD沿BD对折,点A落在E处,BE与CD相交于F,若AD=3,BD=6.
(1)求证:△EDF≌△CBF;
(2)求∠EBC.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南永州卷)数学(解析版) 题型:填空题
如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,求线段CD的长.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南株洲卷)数学(解析版) 题型:选择题
已知反比例函数y= 的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是( )
的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是( )
A.(﹣6,1) B.(1,6) C.(2,﹣3) D.(3,﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com